CV中的Attention
【参考链接】
本文以渣渣的熊猫潘老师的视频课为主体,参考了Bubbliiiing老师的课程中的代码讲解,同时在阅读了原论文后加入了一些自己的心得和体会,本人水平有限,在理解论文内容和两位老师的课程内容过程中,难免有所误解,欢迎交流指正。
1.神经网络学习小记录64——Pytorch 图像处理中注意力机制的解析与代码详解
2.Pytorch 图像处理中注意力机制的代码详解与应用(Bubbliiiing 深度学习 教程)
3.b站up主 渣渣的熊猫潘 CV中的注意力机制
总的来说,注意力机制能够灵活的捕捉全局信息和局部信息之间的联系。它的目的就是让模型获得需要重点关注的目标区域,并对该部分投入更大的权重,突出显著有用特征,抑制和忽略无关特征。
1.通道域注意力机制
1.1 SENet
意义:较早的将attention引入CNN中,模块化设计
CNN的主要作用: 通过系列卷积核提取特征。
对CNN的要求: 优秀的表征能力,但是局部操作有限。
感受野: 卷积神经网络每一层输出的特征图上的像素点对应输入图片上区域大小,似乎要的是全局信息。
增大感受野: 堆叠卷积层、增大卷积核、下采样、空洞卷积等。
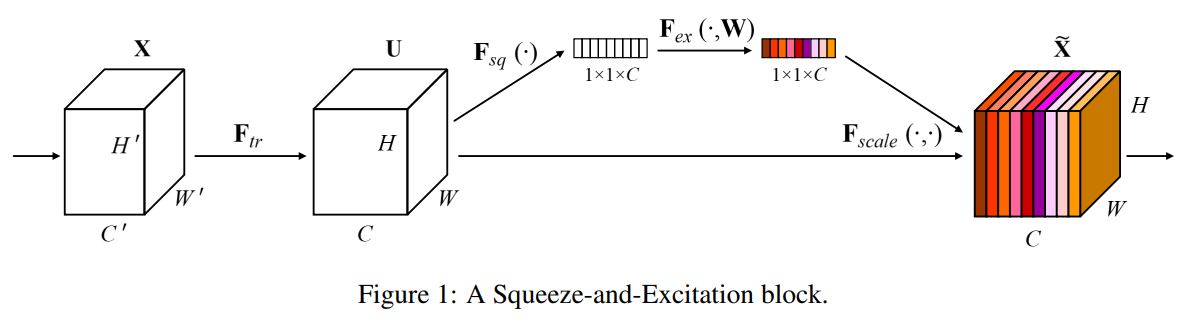
一个目的: 得到一个权重矩阵(核心),对特征进行重构(它是一个可以用来衡量通道重要性的数值,上图中用不同颜色展示)
两个重要操作: Squeeze 和 Excitation
四步走:
Transformation$\mathbf{F}_{t r}$:给定一个input$X\in \mathbb{R} ^{H’\times W’\times C’}$,让其经过$\mathbf{F}_{t r}$做一次映射,得到一个output$U \in \mathbb{R} ^{H\times W\times C}$,即:$U=\mathbf{F}_{t r}(X)$。在传统的CNN中,这一步其实就是一个普通的卷积操作。但是,不同的网络可能有着不同的操作变换。
Squeeze$\mathbf{F}_{s q}$:给定一个input:$U \in \mathbb{R} ^{H\times W\times C}$,让其经过$\mathbf{F}_{s q}$做一次变换,得到一个output:$Z\in \mathbb{R} ^{1\times 1\times C}$:
具体操作:采用全局平均池化(GAP)将每个通道上对应的空间信息$H\times W$压缩到对应通道中变为1个数值,此时1个像素表示一个通道,最终维度变为$1\times 1 \times C$,成了一个向量。
注释: 对$U$实现全局低维嵌入——将空间进行挤压,相当于拥有了全局感受野。
Excitation$\mathbf{F}_{e x}$:给定一个input:$Z\in \mathbb{R} ^{1\times 1\times C}$,让其经过$\mathbf{F}_{e x}$得到一个output:$\mathbf{s}\in \mathbb{R} ^{1\times 1\times C}$
具体操作:将上一步得到的$Z$经过两个全连接层(bottleNeck),对应上面的$\mathbf{W}_{1}$和$\mathbf{W}_{2}$ , 其中$\delta$是激活函数Relu,$\sigma$为激活函数sigmoid,最终得到的$\mathbf{s}$就是我们想得到的权重值。其中$\mathbf{W}_{1}\in \mathbb{R}^{\frac{C}{r}\times C}$,
Scale$\mathbf{F}_{\text {scale }}$:利用上一步得到的权重值,对原始的feature map进
行操作,得到一个output$\widetilde{\mathbf{x}}_{c}\in \mathbb{R} ^{1\times 1\times C}$:
具体操作:将得到的权重施加到$U$上面的每一个通道上。其实也就是对于$U$每个位置上的所有$H\times W$上的值都乘上对应通道的权值而已,完成了特征图的重校准。
应用:
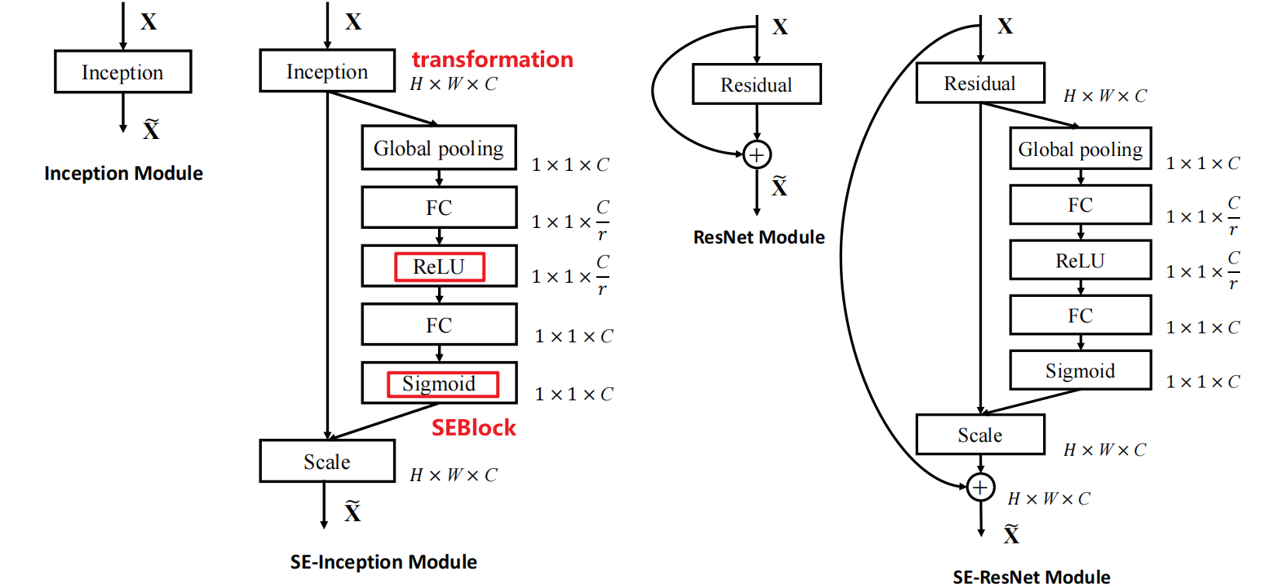
1 | import torch |
1.2 ECANet
问题:SENet破坏了通道与注意力权重之间的关系。
为了分析上述问题,作者设置了3个SENet的变体:SE-Var1、SE-Var2、SE-Var3。
SE-Var1: 没有参数,但是性能优于Besiline,证明了通道注意力机制的确有效。(直接sigmod)
SE-Var2: C 个参数,但是性能优于SE,证明了通道与权重的直接连接很重要。
SE-Var3: $C^2$个参数,性能仍然优于SE,证明了单FC层的跨通道交互比维度削减效果好。
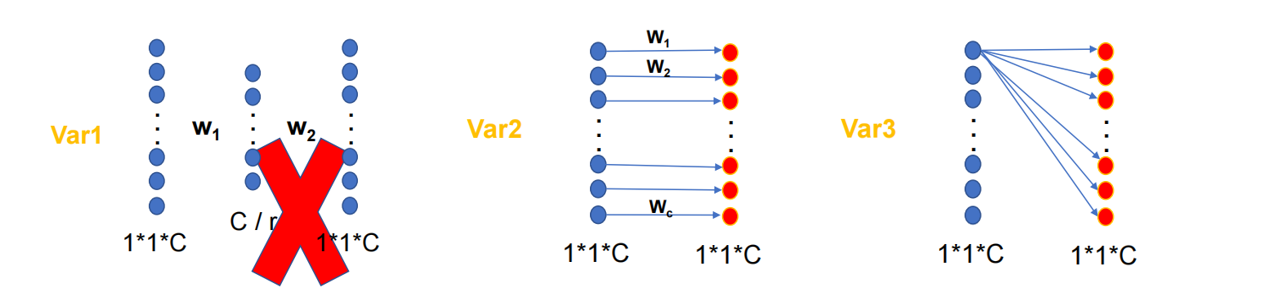

对角矩阵:$\mathbf{W}_{\operatorname{var} 2}$参数量少,但无通道交互。
全矩阵:$\mathbf{W}_{\operatorname{var} 3}$有跨通道交互,但参数量大 。
所以,可以综合$\mathbf{W}_{\operatorname{var} 2}$和$\mathbf{W}_{\operatorname{var} 3}$的优点,采用分组卷积$\mathbf{W}_{G}$(类似于线性代数中的分块矩阵的思想)
但是此时,分组卷积的组与组之间的交互消失了,所以效果并不好,所以作者提出了带状矩阵(参数量为$K\times C$,每行向后平移一个),此时同时保证了信息的交互和参数的减少(类似于一维卷积)
卷积核大小$k$的确定:
$k$和$C$之间应该存在某种对应关系,即:
给定一个$C$,对应的$k$应该为:
其中:$r =2 ,b = 1$,$k$为计算出来临近的奇数值。
具体网络结构如下:
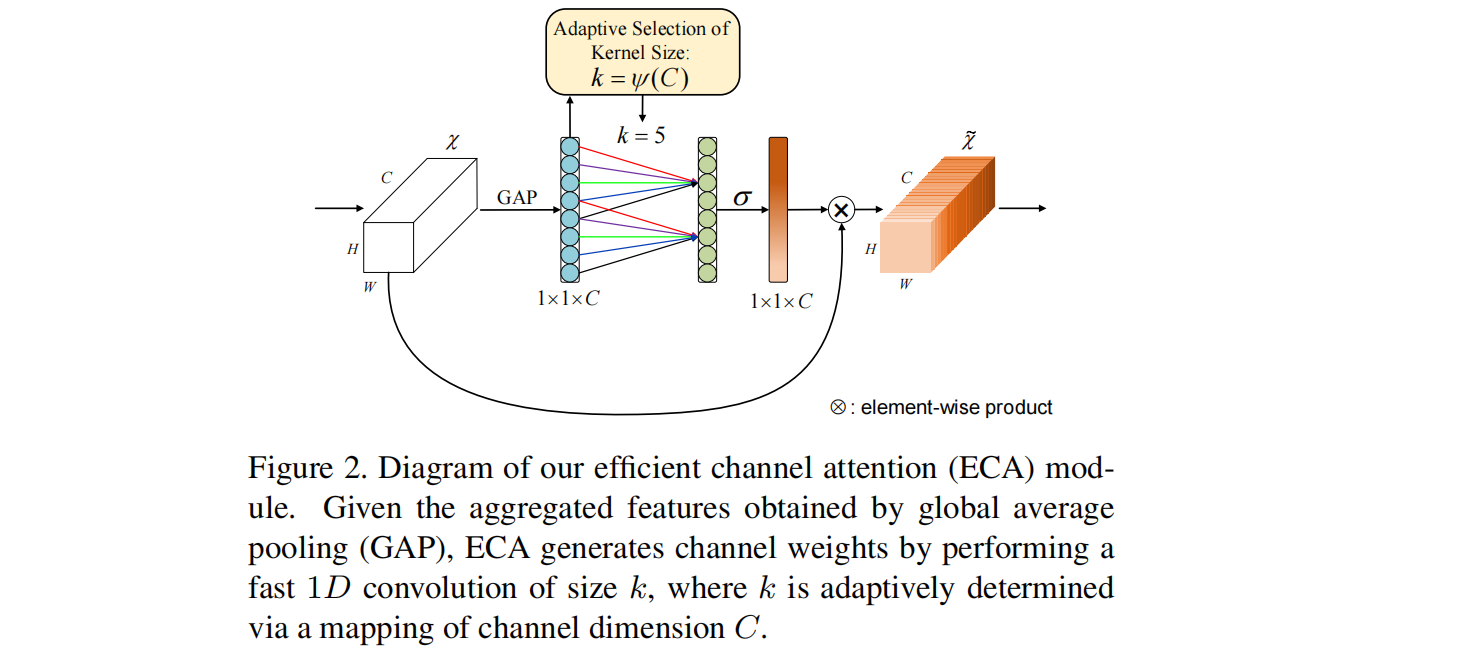
1 | class eca_block(nn.Module): |
1.3 SKNet
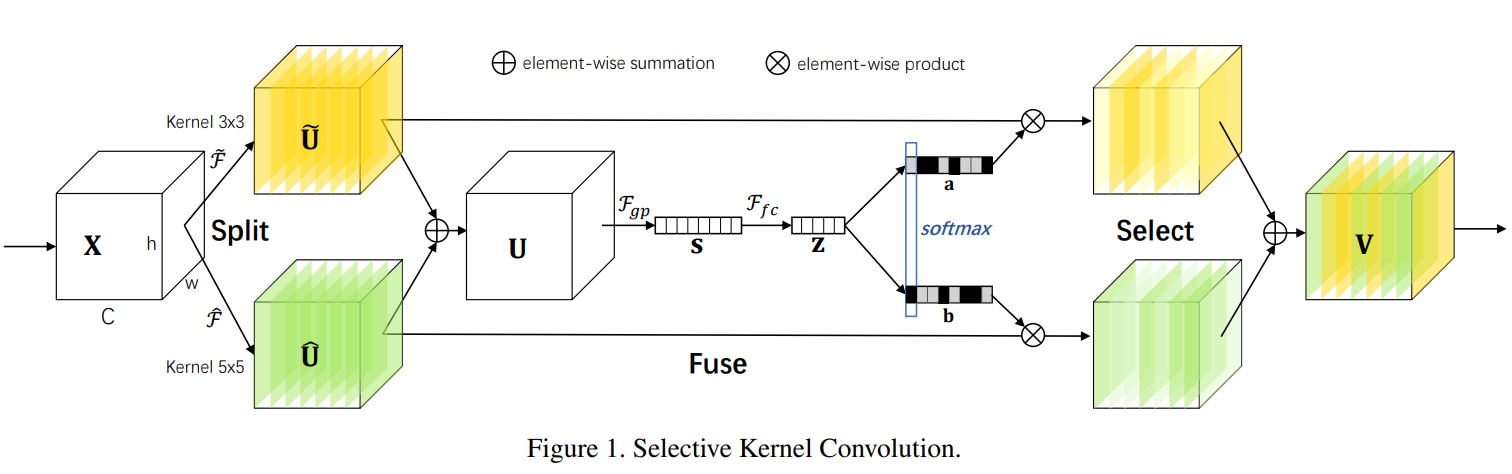
一个目的: 模拟自适应调整感受野——动态重组特征
重要细节: 维度变换、Softmax处
三步走:
- Split:给定一个input,
- Fuse:
- Select
2.混合注意力机制
为什么混合?
不同的维度所代表的意义是不同的,它们本身所携带的信息也是不同的。
- 对于通道而言多数是特征抽象的表达(What)
- 对于空间而言所拥有的位置信息更为丰富(where)。
2.1 BAM
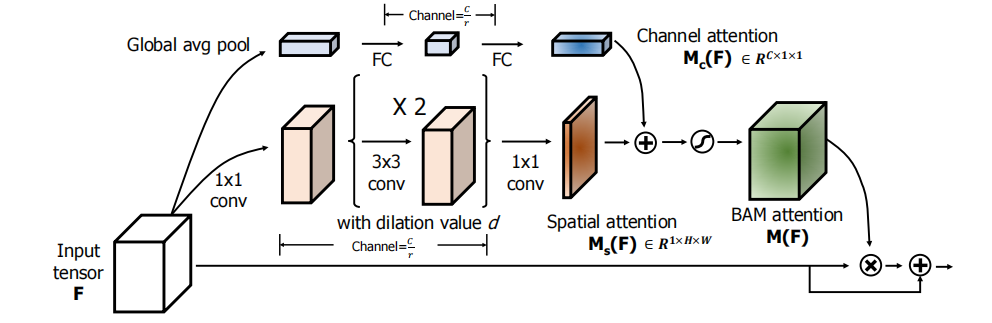
总体架构:
- 给定一个input:$\mathbf{F} \in \mathbb{R} ^{H\times W\times C}$,经过一系列与注意力有关的操作($\mathbf{M}$表示),可以得到一个注意力向量(Attention Vector),即:$\mathbf{F}\in\mathbb{R} ^{H\times W\times C}$
- 上面的$\mathbf{M}$操作包括Channel和Spatial两部分:$\mathbf{M}(\mathbf{F})=\sigma\left(\mathbf{M}_{\mathbf{c}}(\mathbf{F})+\mathbf{M}_{\mathbf{s}}(\mathbf{F})\right)$
- 用上述得到的注意力向量$\mathbf{M}(\mathbf{F})$对原特征图进行重构,即:$\mathbf{F}^{\prime}=\mathbf{F}+\mathbf{F} \otimes \mathbf{M}(\mathbf{F})$
一个目的: 生成混合域的注意力向量——对原特征进行重构
三个分支:
Channel branch :给定一个input,对于$\mathbf{F} \in \mathbb{R} ^{H\times W\times C}$,经过通道注意力SEblock的操作,得到$\mathbf{M_c(F)} \in \mathbb{R} ^{C\times 1\times 1}$,具体的处理方式是:
其中:$\mathbf{W}_{\mathbf{0}} \in \mathbb{R}^{C / r \times C}, \mathbf{b}_{\mathbf{0}} \in \mathbb{R}^{C / r}, \mathbf{W}_{\mathbf{1}} \in \mathbb{R}^{C \times C / r}, \mathbf{b}_{\mathbf{1}} \in \mathbb{R}^{C} $
Spatial branch:给定一个input,对于$\mathbf{F} \in \mathbb{R} ^{H\times W\times C}$,,先进行降维,即经过$1*1$的卷积,然后通过两个${3\times3}$的空洞卷积,再通过${1\times1}$卷积,得到$\mathbf{M_s(F)}\in \mathbb{R} ^{1\times H\times W}$,具体描述如下:
这里采用空洞卷积的目的是增大感受野,另外为了简单化,降维参数设为$C/r$
Combine branch:前面已经提到了通道注意力$\mathbf{M_c(F)}$,空间注意力$\mathbf{M_s(F)}$,现在需要将二者联合起来生成最终的注意力特征图$\mathbf{M(F)}$,需要注意的是二者维度不同,需要都先调整为$\mathbb{R} ^{H\times W\times C}$再进行后续运算,具体操作为:
常见的融合方法有三种: summation, multiplication, max operation 。
重要细节: 不同分支的混合处、维度变换
多BAM构建了一个层次化的注意力,和人类的感知过程很像。
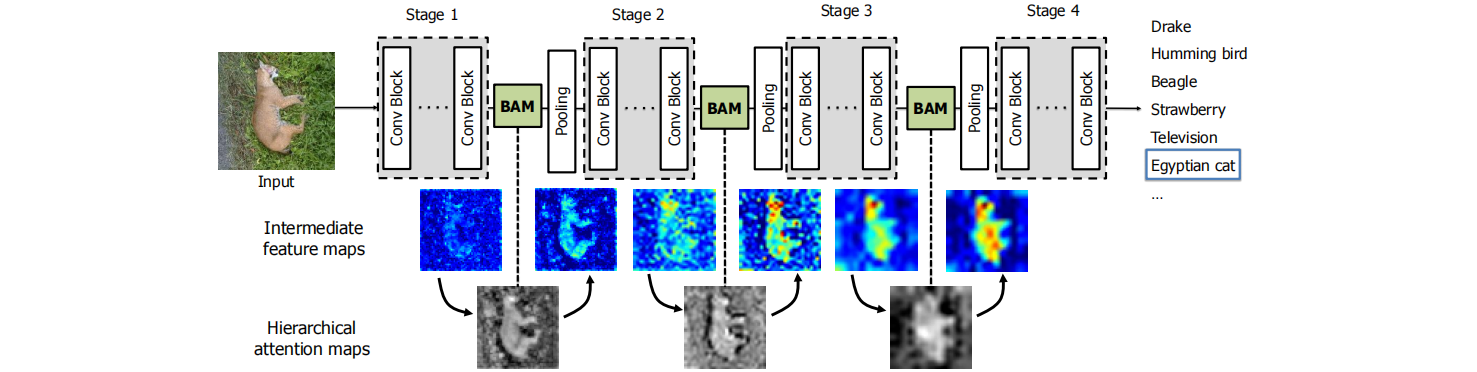
2.2 CBAM
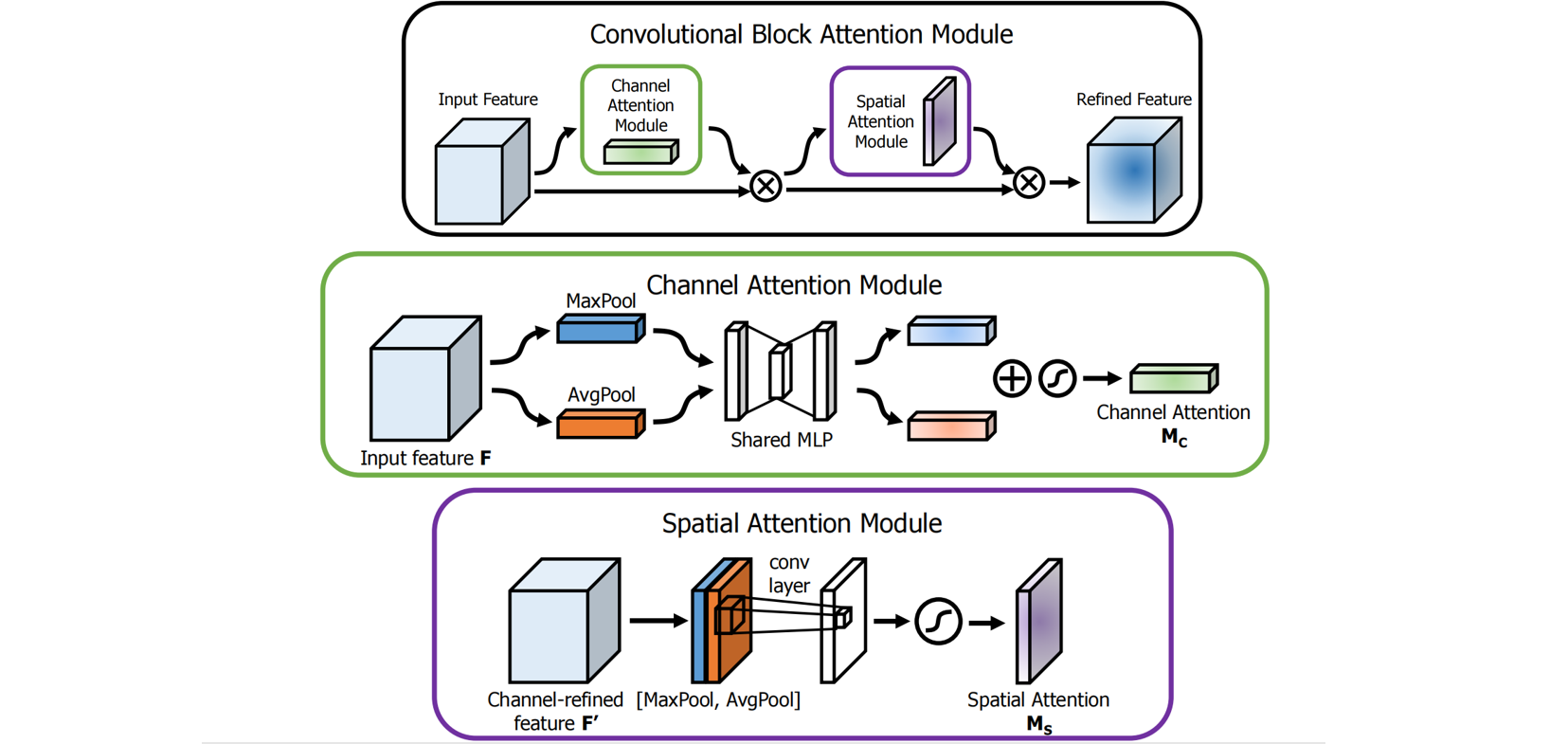
Channel branch :给定一个input,对于$\mathbf{F} \in \mathbb{R} ^{H\times W\times C}$,同时经过全局平均池化(GAP)和全局最大池化(GMP)操作,分别得到不同的空间语义描述算子,将二者通过一个共享感知机,随后将两个通道注意力特征向量使用相加方式进行融合,最后经过激活函数,得到通道注意力向量$\mathbf{M_c} \in \mathbb{R} ^{C\times 1\times 1}$,详细描述如下:
其中,$\sigma$表示sigmod函数,$\mathbf{W}_{\mathbf{0}}\in\mathbb{R} ^{C/r\times C},\mathbf{W}_{\mathbf{1}}\in\mathbb{R} ^{C\times C/r}$,MLP是共享权重的。
Spatial branch : 给定一个input,对于$\mathbf{F} \in \mathbb{R} ^{H\times W\times C}$,沿着通道维度同时经过全局平均池化(GAP)和全局最大池化(GMP)操作,分别得到两种不同的通道特征描述算子,将二者进行拼接,然后经过一个卷积核为${7*7}$的卷积操作,再经过激活函数,最后得到空间注意力向量$\mathbf{M_s} \in \mathbb{R} ^{1\times H\times W}$,详细表述如下:
混合:
- Parallel 并行:通道注意力特征图+空间注意力特征图= 混合混合注意力特征图对原特征图$F$进行校正。
- Sequential串行:通道注意力特征图对原特征图$F$进行矫正=$F’$,空间注意力特征图对特征图$F’$再进行校正。

1 | class ChannelAttention(nn.Module): |