图卷积神经网络的半监督分类(GCN)
1.背景
图结构本身+节点特征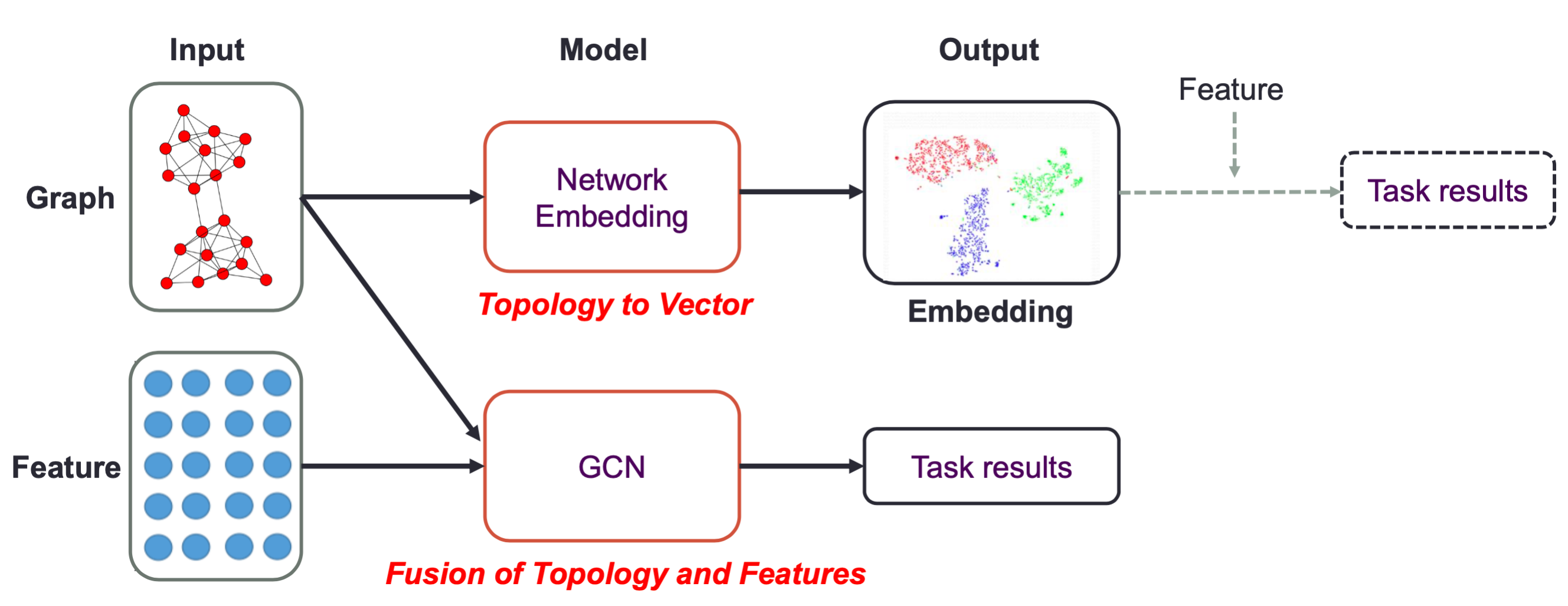
四篇频域核心论文
- ICLR 2014
- ChebyNet (NIPS 2016)
- PATCHY-SAN (ICML 2016)
- Graph Convolutional Network (ICLR 2017)
2.项目成果
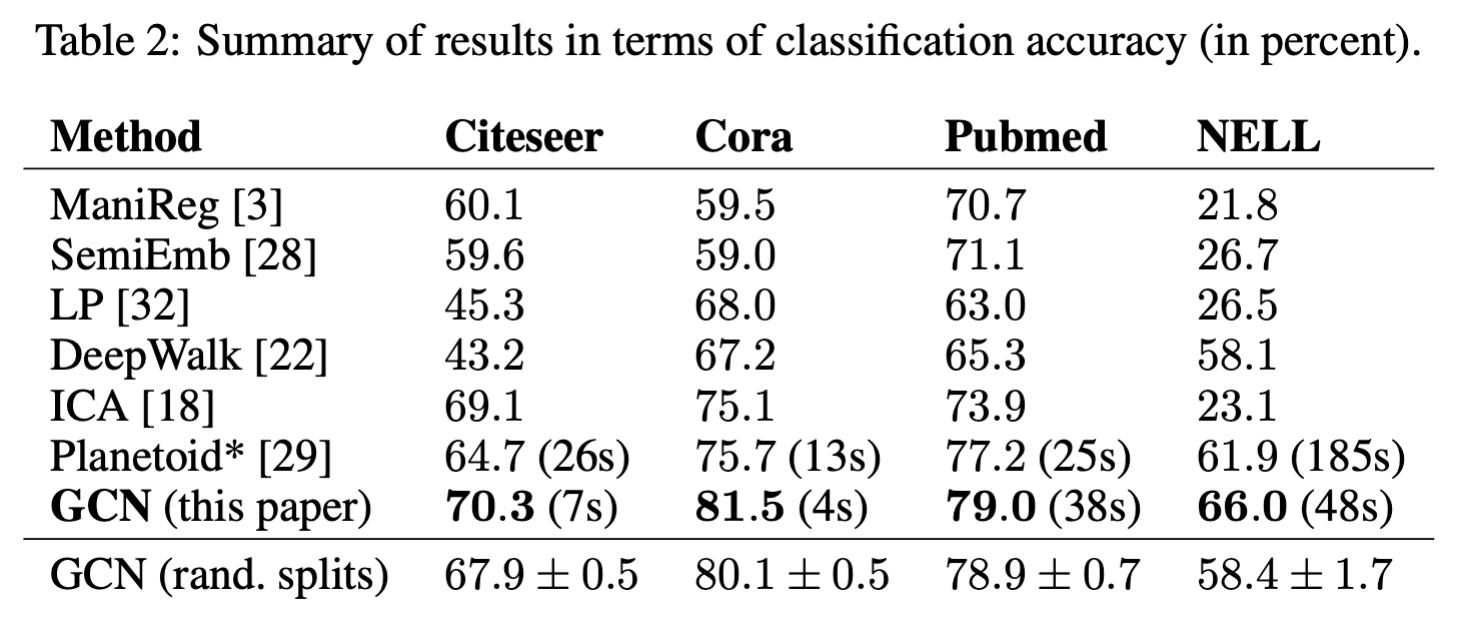

GCN意义
- 卷积神经网络最常用的几个模型之一(GCN,GAT,GraphSAGE)
- 将卷积算法直接用于处理图结构数据,频域分析与消息传播公式
- 图频域卷积的局部一阶近似,单层的GCN处理图中一阶邻居上的信息,K层GCN处理K阶邻居
- 卷积的参数共享,对于每个节点参数是共享的
- 图神经网络的最重要模型之一
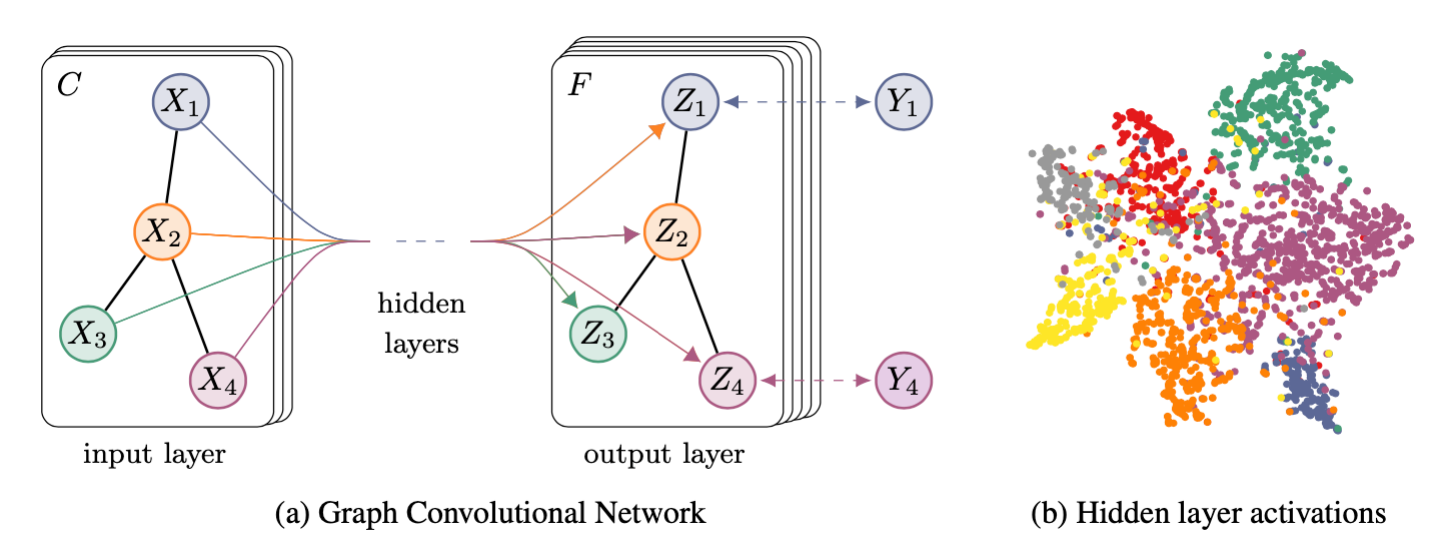
3.GCN结构
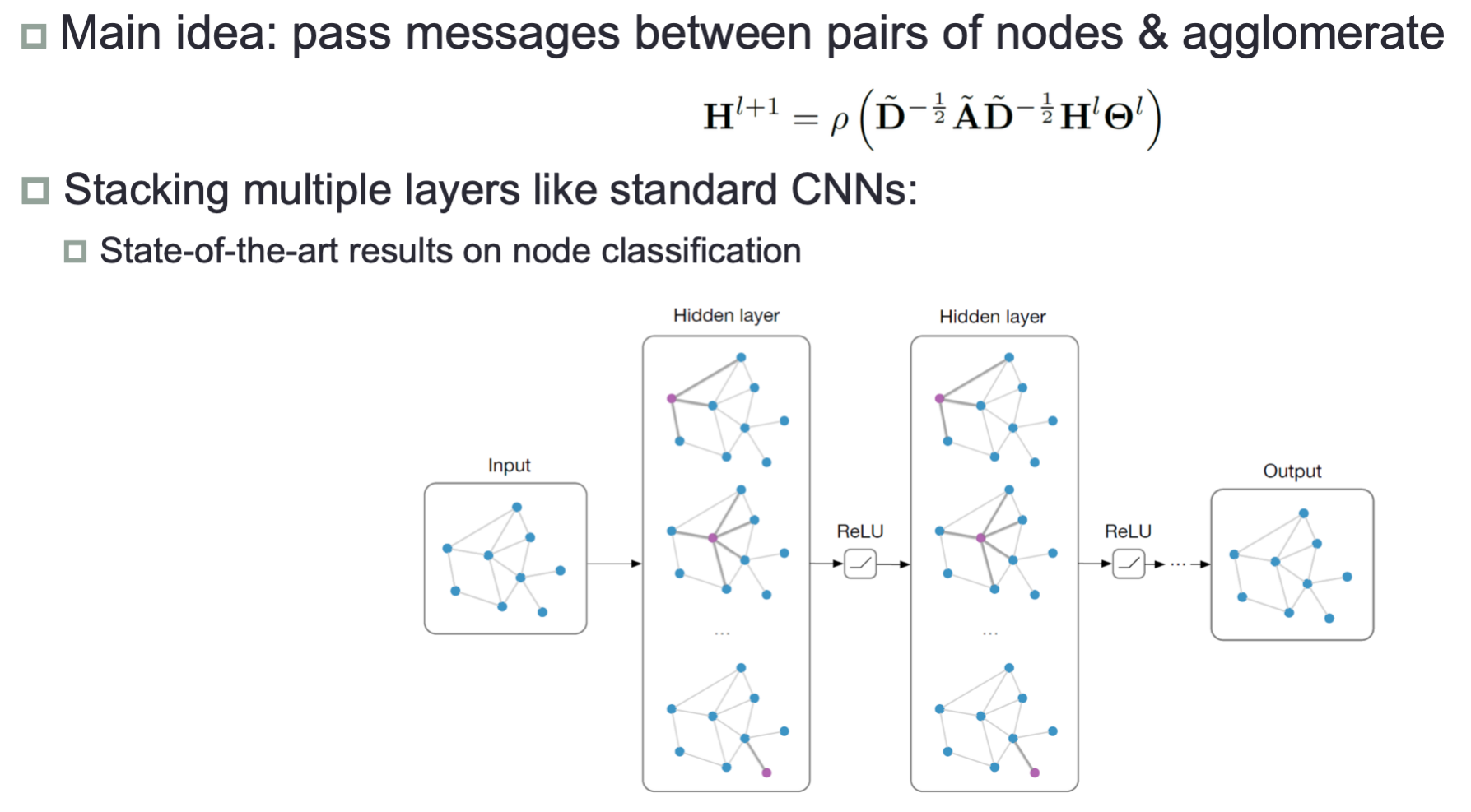
模型框架
$\mathcal{L}=-\sum_{l \in \mathcal{Y}_{L}} \sum_{f=1}^{F} Y_{l f} \ln Z_{l f}$
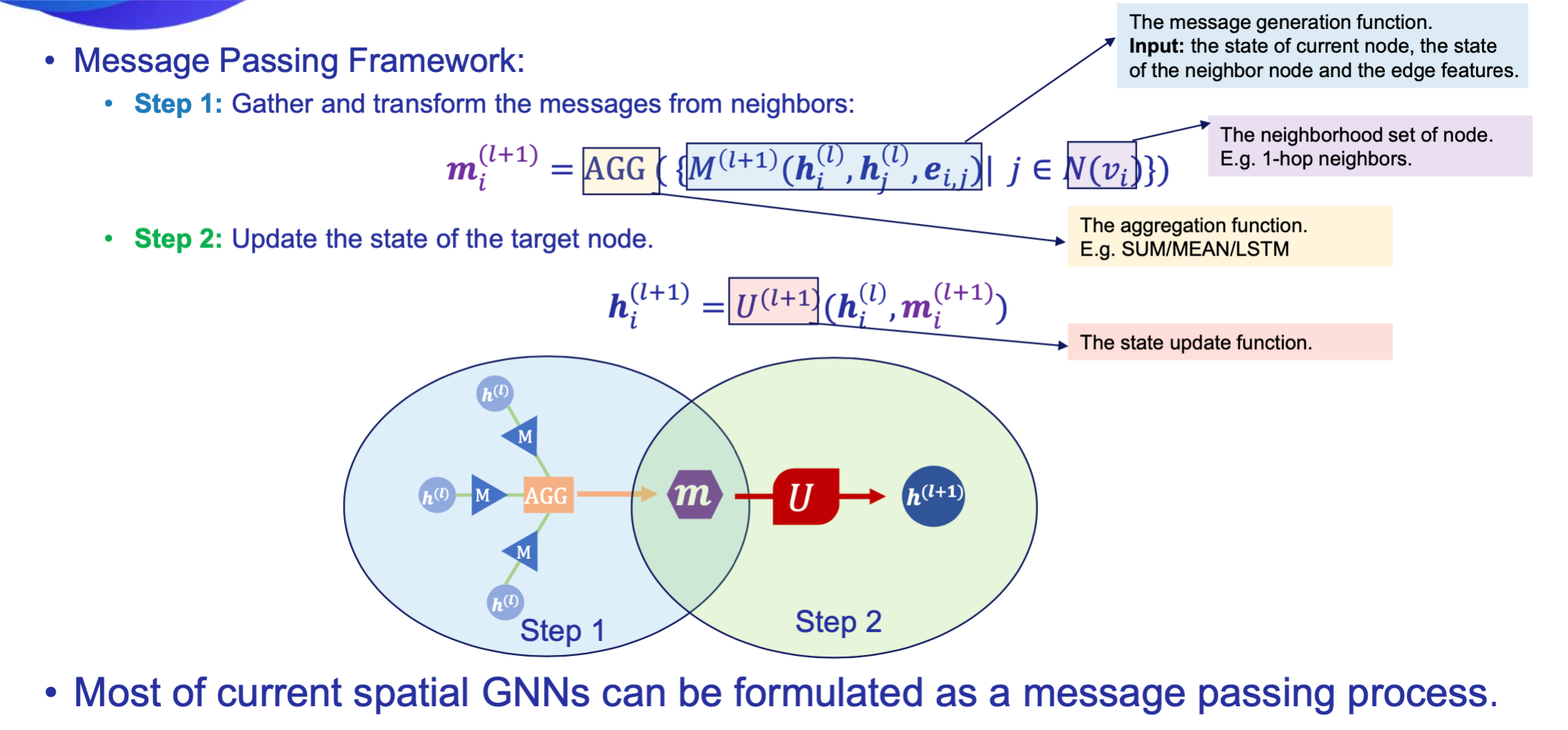
Two major approaches to build Graph CNNs:
- Spatial Domain:
Perform convolution in spatial domain similar to images (euclidean data) with shareable weight parameters - Spectral Domain:
Convert Graph data to spectral domain data by using the eigenvectors of laplacian operator on the graph data
and perform learning on the transformed data.
Graph CNN Summary
- Spatial construction is usually more efficient but less principled.
- Spectral construction is more principled but usually slow. Computing Laplacian eigenvectors for large scale
data could be painful. - Research tries to bridge the gap. (This paper GCN!)
4.RGCN
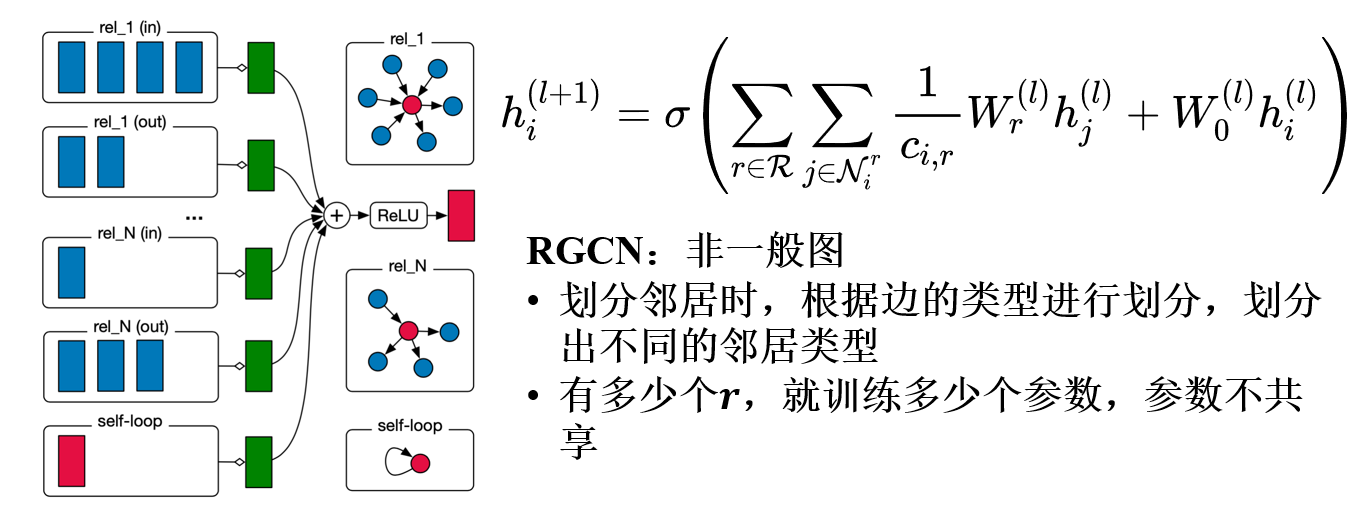
- $N_i^r$表示节点$i$的关系为$r$的邻居节点集合
- $c_{i,r}$是一个正则化常量,其中$c_{i,r}$的取值为$|N_i^r|$
- $W_r^{(l)}$是线性转化函数,将同类型边的邻居节点,使用用一个参数矩阵$W_r^{(l)}$进行转化。
此公式与GCN不同的是,不同边类型所连接的邻居节点,进行一个线性转化,$W_r^{(l)}$的个数也就是边类型的个数,论文中称为relation-specific。当然此处还可以设置更加灵活的函数,例如多层神经网络。
5.拉普拉斯算子
laplacian算子简单的来说就是二阶导数:
那在graph上,我们可以定义一阶导数为:
其中y是x的邻居节点,那么对应的Laplacian算子可以定义为:
拉普拉斯算子: 拉普拉斯算子(Laplace Operator)是$n$维欧几里得空间中的一个二阶微分算子,定义为梯度
($\nabla f$)的散度$\nabla$:
n维形式:
下面推导离散函数的导数:
拉普拉斯矩阵:
如果边$E_{ij}$具有权重$W_{ij}$时,则有:$\Delta f_{i}=\sum_{j \in N_{i}} W_{i j}\left(f_{i}-f_{j}\right)$,由于当$W_{ij}=0$时表示节点$i,j$不相邻,推导有:
其中$d_i=\sum_{j\in N}w_{ij}$是顶点$i$的度。$w_{i:}=\left(w_{i 1}, \ldots, w_{i N}\right)$是$N$维行向量,$\quad f=\left(\begin{array}{c}
f_{1} \\
\vdots \\
f_{N}
\end{array}\right)$是$N$维列向量,$w_{i:}f$表示两个向量的内积,对于所有的$N$个节点有:
所以:
6.拉普拉斯矩阵
拉普拉斯矩阵
对于具有$n$个节点的简单图$G=(V,E)$,若其所有的边都是无向的,那个该图的拉普拉斯矩阵$\mathbf{L} \in \mathbb{R} ^{n\times n}$定义如下:
矩阵的元素如下:
对称归一化拉普拉斯矩阵
定义如下:
矩阵的元素如下:
随机游走归一化拉普拉斯矩阵
定义如下:
矩阵的元素如下:
性质:
- 半正定性
- $n$阶对称矩阵一定有$n$个线性无关的特征向量。
- 对称矩阵的不同特征值对应的特征向量相互正交,这些正交的特征向量构成
的矩阵为正交矩阵。 - 实对称矩阵的特征向量一定是实向量
- 半正定矩阵的特征值一定非负。
- $n$阶对称矩阵一定有$n$个线性无关的特征向量(对称矩阵性质)。$n$维线性空间中的$n$个线性无关的向量都可以构成它的一组基(矩阵论知识)。拉普拉斯矩阵的$n$个特征向量是线性无关的,他们是$n$维空间中的一组基。
- 对称矩阵的不同特征值对应的特征向量相互正交,这些正交的特征向量构成的矩阵为正交矩阵(对称矩阵性质),拉普拉斯矩阵的$n$个特征向量是$n$维空间中的一组标准正交基。
严谨的证明见《Discrete Regularization on Weighted Graphs for
Image and Mesh Filtering》这篇文章。其中定义了在图上如何做梯度运
算和散度运算。
特征向量基的性质:
- 拉普拉斯矩阵的特征值担任了和频率类似的位置。拉普拉斯的特征值都是非负的。且最小特征值为0。类似于经典傅里叶变换中的常数值(可视为频率为0)
- 拉普拉斯矩阵的特征向量担任了基函数的位置。0特征值对应一个常数特征向量,这个和经典傅里叶变换中的常数项类似。低特征值对应的特征向量比较平滑,高特征值对应的特征向量变换比较剧烈。两者对应于低频基函数和高频基函数。
- 通过定义图拉普拉斯二次型 (graph Laplacian quadratic form)来定义信号的平滑程度。其表示有边相连的两个节点信号的平方差乘以边的权重后求和。其值越小,代表信号$x$越平滑:$x^{T} L x=1 / 2 \sum_{i, j=1}^{m} W_{i, j}(x(i)-x(j))^{2}$。当特征向量带入这个函数时,二次型的值等于特征值。这恰好是符合经典傅里叶变换中的频率
设定——频率越高,基函数(余弦函数)变化越陡峭。
7.傅里叶变换
Convolution的数学定义是:
一般称$g$为作用在$f$上的filter或kernel
根据卷积定理,卷积公式还可以写成
这样我们只需要定义graph上的fourier变换,就可以定义出graph上的convolution变换。
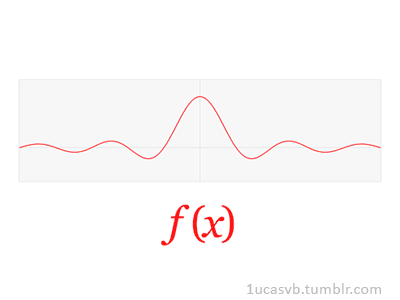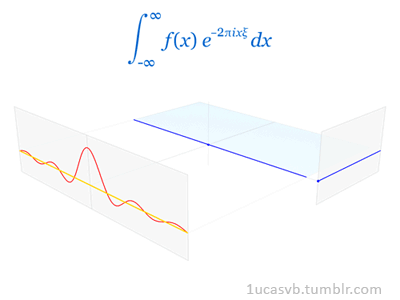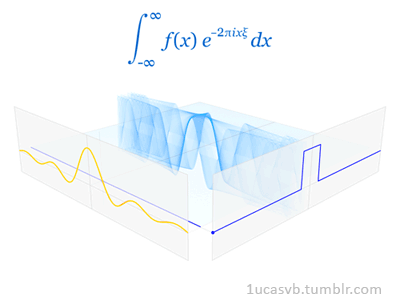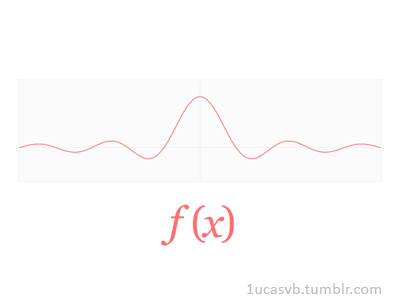
Fourier变换的定义:
Inverse Fourier变换则是:
- 傅里叶反变换的本质是:把任意一个函数表示成了若干个正交基函数的线性组合。
- 傅里叶正变换的本质是:求线性组合的的系数。具体做法是由原函数和基函数的
共轭的内积求得。
根据特征值和特征向量的关系:
对$e^{-i \omega t}$做拉普拉斯算子:
可以将$\Delta$比作特征值公式中的$\mathbf{A}$,将$-\omega^{2}$比作$\lambda$,可以完全对应特征值与特征向量的关系,即$e^{-i \omega t}$是拉普拉斯算子的特征向量。类比到图中,图的拉普拉斯矩阵的特征向量,也可以作为图的傅里叶变换的基。
图矩阵到图频域的正变换:
图频域到图矩阵的逆变换:
8.卷积定理
定理内容:
证明:
约定:
所以,可以得到:
9.图表示总结
Starting from signal processing:
- Recall that: The Laplacian is indeed diagonalized by the Fourier basis
(the orthonormal eigenvectors)$U=[u_1,u_2,\dots u_{N-1}]\in \mathbb{R}^{N\times N}$ - Let$\Lambda =\text{diag}([\lambda _0,\dots \lambda _{N-1} ]) $, then we have$L=U\Lambda U^T$
- recall that$ \mathcal{X} \otimes \mathcal{Y}= Fourier _{\text {inverse }}( Fourier (\mathcal{X}) \odot Fourier (\mathcal{Y}) ) $
- Definition of convolutional operator:$(f h)( \mathcal{G})=U\left(\left(U^{T} f\right) \odot\left(U^{T} h\right)\right)$
Graph Laplacian another expression:
where $\lambda_i$ is eigenvalue,and $U=(\overrightarrow{u_0} ,\overrightarrow{u_1},\dots \overrightarrow{u_N}) $,$\overrightarrow{u_i}$is column vector, and
is unit eigenvector,$U^{-1}$could be replaced by$U^T$,because$UU^T=I_N$,Fourier transformation could be expressed as:
10.三个经典图谱卷积模型
简介
- 三个图谱卷积模型(SCNN、ChebNet、GCN)均立足于谱图理论且一脉相承。
- ChebNet可看做SCNN的改进,GCN可看做ChebNet的改进。
- 三个模型均可认为是下式的一个特例。
11.GCN卷积核1—SCNN
核心思想:用可学习的对角矩阵来代替谱域的卷积核,从而实现图卷积操作。
《Spectral Networks and Deep Locally Connected Networks on Graphs》的方法:
- 计算复杂度高,计算复杂度为为$O(n^3)$n为节点个数。当处理大规模图数据时(比如社交网络数据,通常有上百万个节点)会面临很大的挑战。
- n个参数,计算复杂度为$O(n)$,当节点数较多时容易过拟合。
- 无localization
具体公式如下:
- 其中,$C_k$表示第$k$层的channel通道个数,$x_{k,i}\in \mathbb{R}^n$表示第k层的第i个channel的feature map(特征图)
- $F_{k,i,j}\in \mathbb{R}^{n\times n}$代表参数化的谱域的卷积核矩阵。 它是一个对角矩阵,包含了$n$个可学习的参数。$h(.)$表示激活函数
- 假设输入 channel 和输出channel 为 1。简化版本的SCNN卷积公式如下:$x_{k+1}=h\left(U F_{k} U^{T} x_{k}\right) \quad x_{k+1} \in \mathbb{R}^{n}, x_{k} \in \mathbb{R}^{n}$
12.GCN卷积核2
《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》的方法:
无需对角化的证明:
- 无需特征分解
- K个参数<n
- localization
13.GCN切比雪夫卷积核—ChebNet
《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》的方法:
其中,由于切比雪夫多项式的定义域问题,进行归一化:$\tilde{\Lambda}=2\Lambda/\lambda_{max}-I$,将定义域变为$2\times[0,1]-1$,同理,$\tilde{L}=2L/\lambda_{max}-I$,,可以得到$y=\sigma\left(U \sum_{k=0}^{K-1} \beta_{k} T_{k}(U\tilde{\Lambda}U^{T}) x\right)$,或表示为$y=\sigma\left(U \sum_{k=0}^{K-1} \beta_{k} T_{k}(\tilde{L}) x\right)$,同时切比雪夫多项式满足递推公式:$T_k(\tilde{L})=2\tilde{L}T_{k-1}(\tilde{L})-T_{k-2}(\tilde{L})$,其中$T_0(\tilde{L})=I,T_1(\tilde{L})=\tilde{L}$
【例】
递推公式中第一项的卷积核:
第二项的卷积核:其中$L^{sys}=I-D^{-0.5}AD^{-0.5}$
特点:
卷积核只有$k+1$个可学习的参数,一般 $k$远小于$n$,参数的复杂度被大大降低
采用Chebyshev多项式代替谱域的卷积核后,经过公示推导,ChebNet不需
要对拉普拉斯矩阵做特征分解了。省略了最耗时的步骤。卷积核具有严格的空间局部性。同时,$k$就是卷积核的“感受野半径”。即将
中心顶点$k$阶近邻节点作为邻域节点。
14.GCN卷积核简化-GCN
仅仅考虑一阶切比雪夫多项式。$T_{0}(\hat{L})=I \quad T_{1}(\hat{L})=\hat{L},\hat{L}=\frac{2}{\lambda_{\max }} L-I_{n},
\lambda_{\max }=2,L=I_{n}-D^{-1 / 2} W D^{-1 / 2}
$
进一步简化,使得每个卷积核只有一个可学习的参数。令$
\beta_{0}=-\beta_{1}=\theta$那么$
\quad x \star_{G} g_{\theta}=\left(\beta_{0}-\beta_{1}\left(D^{-1 / 2} W D^{-1 / 2}\right)\right) x=\left(\theta\left(D^{-1 / 2} W D^{-1 / 2}+I_{n}\right)\right) x
$
renormalization trick:因为$D^{-1 / 2} W D^{-1 / 2}+I_{n}$有范围[0,2]的特征值,如果在深度神经网络模型中使
用该算子,则反复应用该算子会导致数值不稳定(发散)和梯度爆炸/消失,
为了解决该问题, 引入了一个 renormalization trick
最终公式:
- 在忽略input channel 和 output channel的情况下,卷积核只有1个可学习
的参数,极大的减少了参数量。(按照作者的说法:“We intuitively expect that such a model can alleviate
the problem of overfitting on local neighborhood structures for graphs with very wide node degree distributions, such as
socialnetworks, citation networks, knowledge graphs and many other real-world graph datasets.”) - 虽然卷积核大小减少了(GCN仅仅关注于一阶邻域,类似于3X3的经典卷积),
但是作者认为通过多层堆叠GCN,仍然可以起到扩大感受野的作用。 - 与此同时,这样极端的参数削减也受到一些人的质疑。他们认为每个
卷积核如果只设置一个可学习参数,会降低模型的能力。(可以参考博文
How powerful are Graph Convolutions? )如果将传统图像的每一个像素视为graph的一个节点,节点之间为八邻域链接,图像也可以看做一张特殊的图。那么在每个3*3的卷
积核里,仅仅存在1个可学习的参数。从目前应用在image的深度学习经验看来,这样的卷积模型复杂度虽然低,但是模型的能力也遭到了削弱,可能难以处理复杂的任务。