pytorch日积月累-梯度与自动求导

pytorch日积月累4-梯度与自动求导

1.深度学习的核心——梯度

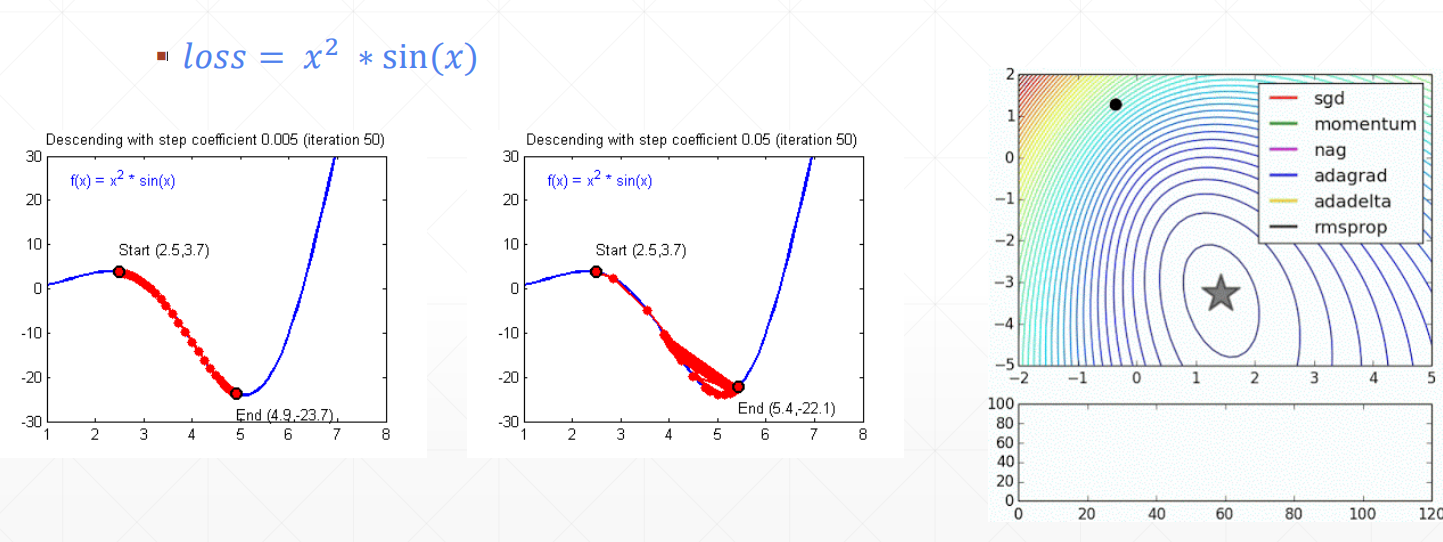
learnrate：学习率，迭代速度的限制因素。

设置不同的梯度下降的求解器

$$loss=(WX+b-y)^2\\ w'=w-lr\times \frac{\bigtriangledown loss }{\bigtriangledown w}$$

import numpy as np
def compute_error_for_line_given_points(b,w,points):
    totalError=0
    for i in range(0,len(points)):
        x=points[i,0]#取x值
        y=points[i,1]#取y值
        totalError+=(y-(w*x+b))**2
    return totalError/float(len(points))#做平均
def step_gradient(b_current,w_current,points,learningRate):
    b_gradient=0
    w_gradient=0
    N=float(len(points))
    for i in range(0,len(points)):
        x = points[i, 0]  # 取x值
        y = points[i, 1]  # 取y值
        #通过数学方法计算出求导公式，然后代入计算。
        b_gradient+=-(2/N)*(y-((w_current*x)+b_current))#对b求导
        w_gradient+=-(2/N)*x*(y-((w_current*x)+b_current))#对w求导
    new_b=b_current-(learningRate*b_gradient)
    new_w=w_current-(learningRate*w_gradient)
    return [new_b,new_w]
def gradient_descent_runner(points,starting_b,starting_w,
                            learing_rate,num_iterations):
    b=starting_b
    w=starting_w
    for i in range(num_iterations):
        b,m=step_gradient(b,w,np.array(points),learing_rate)
    return [b,m]

2.随机梯度

2.1什么是梯度

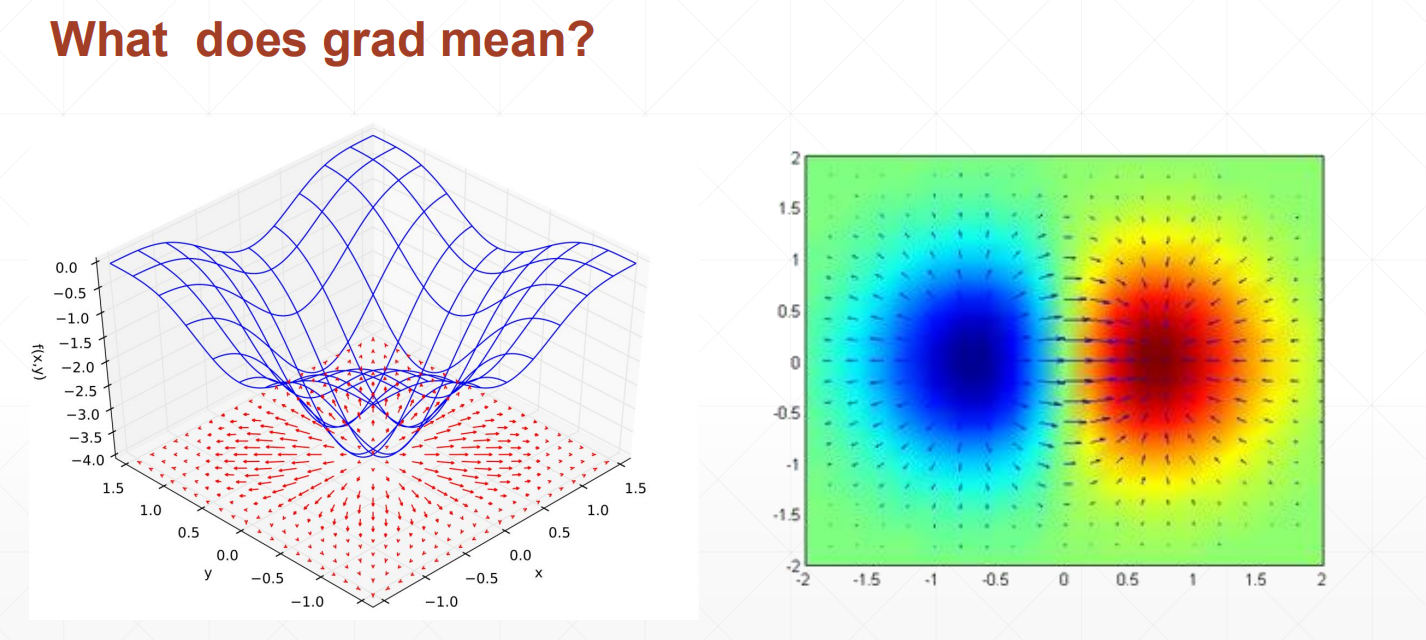
Optimizer Performance

▪ initialization status（初始值）

▪ learning rate（学习率）

▪ momentum（动量，惯性）

2.2激活函数及其梯度

激活函数：

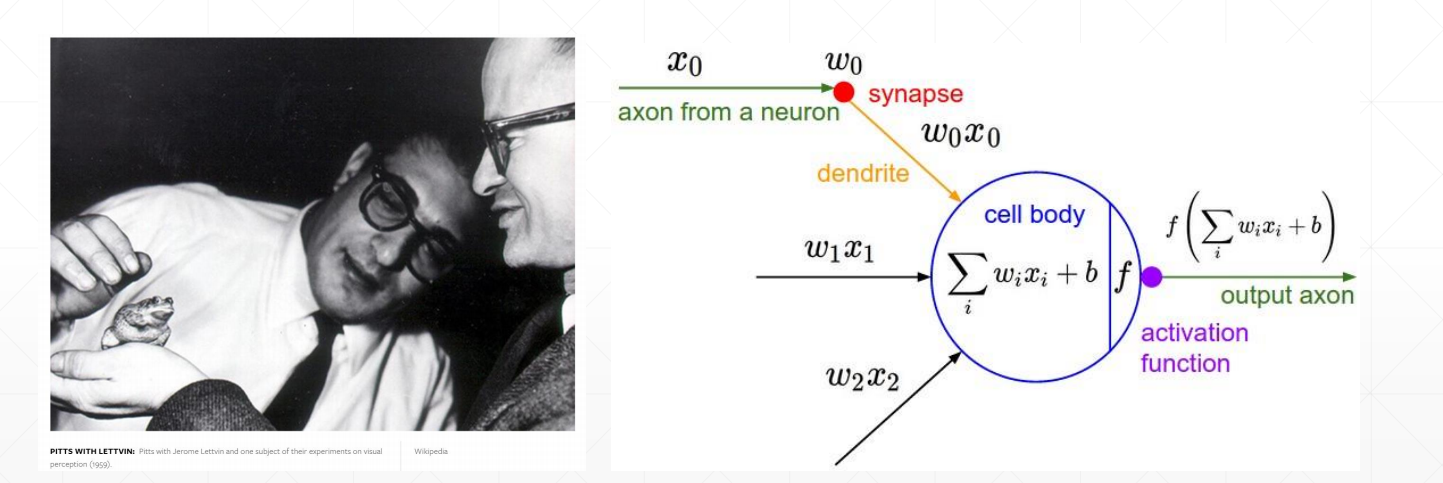
最简单的激活函数：

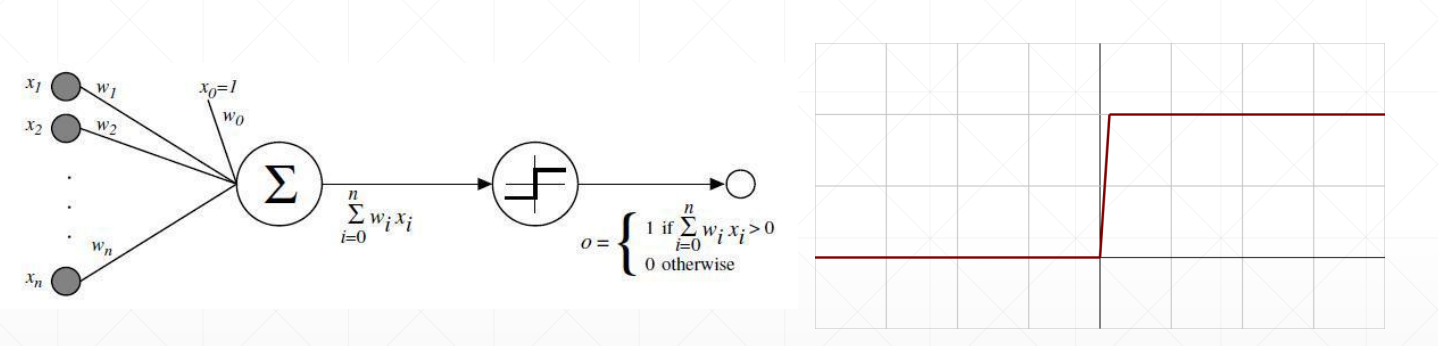
Sigmoid / Logistic函数——光滑可导

$$\begin{aligned} \frac{d}{d x} \sigma(x) &=\frac{d}{d x}\left(\frac{1}{1+e^{-x}}\right) \\ &=\frac{e^{-x}}{\left(1+e^{-x}\right)^{2}} \\ &=\frac{\left(1+e^{-x}\right)-1}{\left(1+e^{-x}\right)^{2}} \\ &=\frac{1+e^{-x}}{\left(1+e^{-x}\right)^{2}}-\left(\frac{1}{1+e^{-x}}\right)^{2} \\ &=\sigma(x)-\sigma(x)^{2} \\ \sigma^{\prime} &=\sigma(1-\sigma) \end{aligned}$$

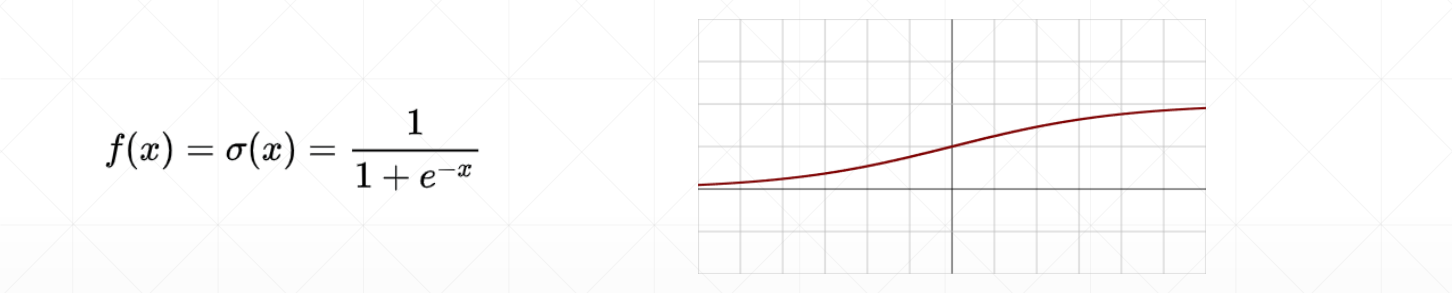
import torch
a=torch.linspace(-100,100,10)
torch.sigmoid(a)

Tanh——RNN中用的较多

$$\begin{array}{l} \frac{d}{d x} \tanh (x)=\frac{\left(e^{x}+e^{-x}\right)\left(e^{x}+e^{-x}\right)-\left(e^{x}-e^{-x}\right)\left(e^{x}-e^{-x}\right)}{\left(e^{x}+e^{-x}\right)^{2}} \\ =1-\frac{\left(e^{x}-e^{-x}\right)^{2}}{\left(e^{x}+e^{-x}\right)^{2}}=1-\tanh ^{2}(x) \end{array}$$

import torch
a=torch.linspace(-1,1,10)
torch.tanh(a)

Rectified Linear Unit——RELU——非线性激活函数

$$f^{\prime}(x)=\left\{\begin{array}{ll} 0 & \text { for } x<0 \\ 1 & \text { for } x \geq 0 \end{array}\right.$$

from torch.nn import functional as F
a=torch.linspace(-1,1,10)
torch.relu(a)
F.relu(a)

2.3LOSS及其梯度

Mean Squared Error(MSE)

$$\begin{array}{l} \operatorname{loss} =\sum[y-(x w+b)]^{2} \\ L 2-\operatorname{norm}=|| y-(x w+b)||_{2} \\ \operatorname{loss} =\operatorname{norm}(y-(x w+b))^{2} \end{array}$$

Derivative

$$\operatorname{loss} =\sum\left[y-f_{\theta}(x)\right]^{2} \\ \frac{ { \nabla loss }}{\nabla \theta}=2 \sum\left[y-f_{\theta}(x)\right] \times \frac{\nabla f_{\theta}(x)}{\nabla \theta}$$

• torch.autograd.grad(loss, [w1, w2,…])——->[w1 grad, w2 grad…]

• loss.backward() —-> w1.grad w2.grad

x=torch.ones(1)
w=torch.full([1],2)
w.requires_grad_()#更新w的信息为可求导的
mse=F.mse_loss(torch.ones(1),x*w)#重新绘制动态图
torch.autograd.grad(mse,[w])

softmax

$$p_{i}=\frac{e^{a_{i}}}{\sum_{k=1}^{N} e^{a_{k}}}$$ $$when \ i=j \begin{aligned} \frac{\partial \frac{e^{a_{i}}}{\sum_{k=1}^{N} e^{a_{k}}}}{\partial a_{j}} &=\frac{e^{a_{i}} \sum_{k=1}^{N} e^{a_{k}}-e^{a_{j}} e^{a_{i}}}{\left(\sum_{k=1}^{N} e^{a_{k}}\right)^{2}} \\ &=\frac{e^{a_{i}}\left(\sum_{k=1}^{N} e^{a_{k}}-e^{a_{j}}\right)}{\left(\sum_{k=1}^{N} e^{a_{k}}\right)^{2}} \\ &=\frac{e^{a_{j}}}{\sum_{k=1}^{N} e^{a_{k}}} \times \frac{\left(\sum_{k=1}^{N} e^{a_{k}}-e^{a_{j}}\right)}{\sum_{k=1}^{N} e^{a_{k}}} \\ &=p_{i}\left(1-p_{j}\right) \end{aligned}$$ $$when\ \ \ i \neq j \begin{aligned} \frac{\partial \frac{e^{a_{i}}}{\sum_{k=1}^{N} e^{a_{k}}}}{\partial a_{j}} &=\frac{0-e^{a_{j}} e^{a_{i}}}{\left(\sum_{k=1}^{N} e^{a_{k}}\right)^{2}} \\ &=\frac{-e^{a_{j}}}{\sum_{k=1}^{N} e^{a_{k}}} \times \frac{e^{a_{i}}}{\sum_{k=1}^{N} e^{a_{k}}} \\ &=-p_{j} \cdot p_{i} \end{aligned}$$

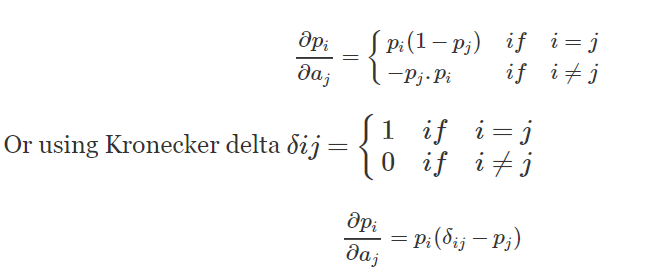
2.4利用pytorch实现线性回归

import torch
import matplotlib.pyplot as plt
torch.manual_seed(10)
lr = 0.05  # 学习率    20191015修改
# 创建训练数据
x = torch.rand(20, 1) * 10  # x data (tensor), shape=(20, 1)
y = 2*x + (5 + torch.randn(20, 1))  # y data (tensor), shape=(20, 1)
# 构建线性回归参数
w = torch.randn((1), requires_grad=True)
b = torch.zeros((1), requires_grad=True)#随机初始化可求导
for iteration in range(1000):
    # 前向传播
    wx = torch.mul(w, x)
    y_pred = torch.add(wx, b)
    # 计算 MSE loss
    loss = (0.5 * (y - y_pred) ** 2).mean()
    # 反向传播
    loss.backward()
    # 更新参数
    b.data.sub_(lr * b.grad)
    w.data.sub_(lr * w.grad)

3.自动求导

3.1torch.autograd

• torch.autograd.backward
• 功能：自动求取梯度
• 函数说明如下：

#第一个常用的函数
torch.autograd.backward(tensors,
                        grad_tensors=None,#多梯度权重
                        retain_graph=None,#保存计算图
                        create_graph=False)#创建导数计算图，用于高阶求导

使用反向传播计算梯度：

• retain_graph=True用于保存动态图

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)
y.backward(retain_graph=True)
print(w.grad)
y.backward()

• gradient=grad_tensors用于多个梯度之间的权重计算

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)     # retain_grad()
b = torch.add(w, 1)
y0 = torch.mul(a, b)    # y0 = (x+w) * (w+1)
y1 = torch.add(a, b)    # y1 = (x+w) + (w+1)    dy1/dw = 2
loss = torch.cat([y0, y1], dim=0)       # [y0, y1]
grad_tensors = torch.tensor([1., 2.])
loss.backward(gradient=grad_tensors)    
# gradient 传入 torch.autograd.backward()中的grad_tensors
print(w.grad)

• torch.autograd.grad
• 功能：求取梯度
• 函数说明如下：

torch.autograd.grad(outputs,#用于求导的张量
                    inputs,#需要梯度的张量
                    grad_tensors=None,#多梯度权重
                    retain_graph=None,#保存计算图
                    create_graph=False)#创建导数计算图，用于高阶求导

x = torch.tensor([3.], requires_grad=True)
y = torch.pow(x, 2)     # y = x**2
grad_1 = torch.autograd.grad(y, x, create_graph=True)   
# grad_1 = dy/dx = 2x = 2 * 3 = 6
print(grad_1)
grad_2 = torch.autograd.grad(grad_1[0], x)              
# grad_2 = d(dy/dx)/dx = d(2x)/dx = 2
print(grad_2)

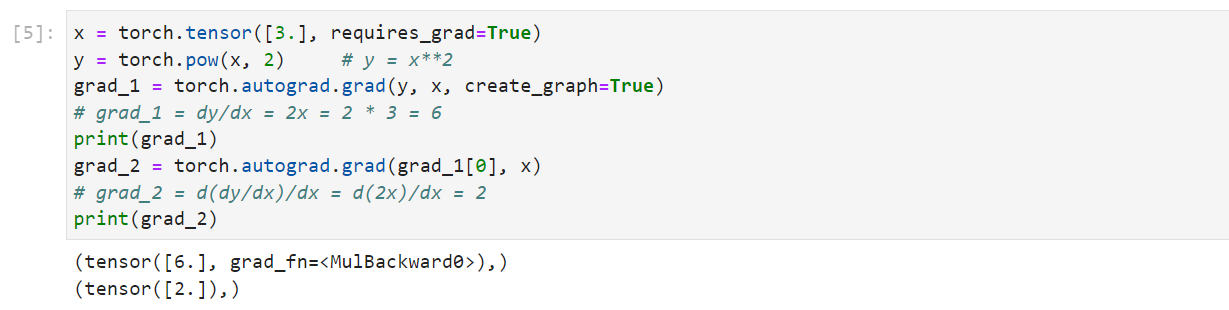
autograd小贴士：

• 梯度不自动清零

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
for i in range(4):
    a = torch.add(w, x)
    b = torch.add(w, 1)
    y = torch.mul(a, b)
    y.backward()
    print(w.grad)

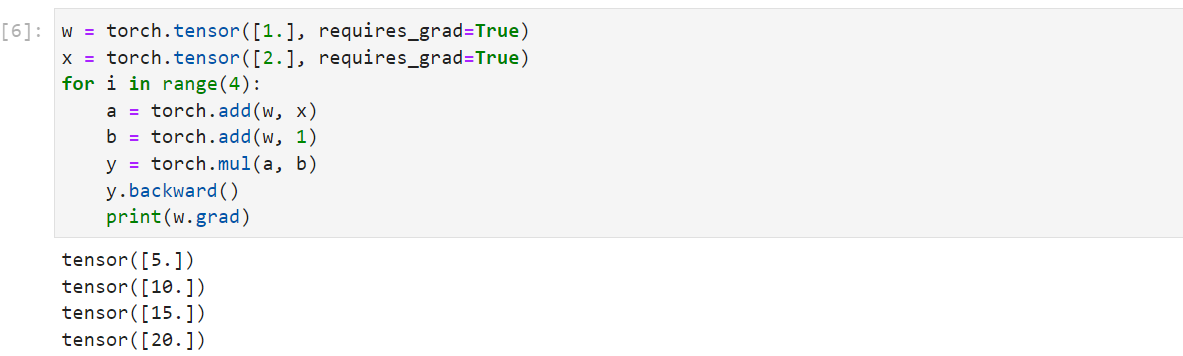
• 依赖于叶子结点的结点，requires_grad默认为True
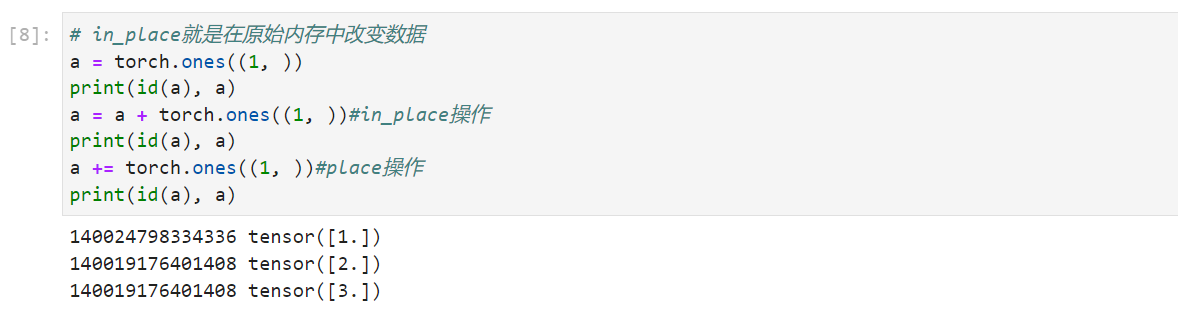
• 叶子结点不可执行in-place

a = torch.ones((1, ))
print(id(a), a)
a = a + torch.ones((1, ))#in_place操作
print(id(a), a)
a += torch.ones((1, ))#place操作
print(id(a), a)

3.2逻辑回归

利用pytorch生成训练的数据

import torch
import torch.nn as nn
import matplotlib.pyplot sas plt
import numpy as np
#step1:数据
sample_nums=100
mean_value=1.7
bias=100
n_data=torch.ones(sample_nums,2)
x0=torch.normal(mean_value*n_data,1)+bias     #类别0 数据shape=(100,2)
y0=torch.zeros(sample_nums)                   #类别0 标签shape=(100,1)
x1=torch.normal(-mean_value*n_data,1)+bias    #类别1 数据shape=(100,2)
y0=torch.zeros(sample_nums)                   #类别1 标签shape=(100,1) 
train_x=torch.cat((x0,x1),0)
train_y=torch.cat((y0,y1),0)

选择模型：

#step2:模型
#定义逻辑回归中的前向传播算法
class LR(nn.Module):
    def __init__(self):#继承自nn.Module类
        super(LR,self).__init__()
        self.features=nn.Linear(2,1)
        self.sigmoid=nn.Sigmoid()
    def forward(self,x):
        x=self.features(x)
        x=self.sigmoid(x)
        return x
#实例化逻辑回归模型
lr_net=LR()

定义损失函数：

#step3:损失函数
loss_fn=nn.BCELoss()#交叉熵损失函数

定义优化器：

#step4:优化器
lr=0.01
optimizer=torch.optim.SGD(lr_net.parameters(),lr=lr,momentum=0.9)
#使用随机梯度下降的优化器

迭代训练模型

#step5:迭代训练
for iteration in range(100):
    y_pred=lr_net(train_x)#前向传播
    loss=loss_fn(y_pred.squeeze(),train_y)#计算loss
    loss.backward()#反向传播
    optimizer.step()#更新参数
    optimizer.zero_grad()#清空梯度
    if iteration % 20 == 0:
        mask = y_pred.ge(0.5).float().squeeze()  # 以0.5为阈值进行分类
        correct = (mask == train_y).sum()  # 计算正确预测的样本个数
        acc = correct.item() / train_y.size(0)  # 计算分类准确率
        plt.scatter(x0.data.numpy()[:, 0], x0.data.numpy()[:, 1], 
                    c='r', label='class 0')
        plt.scatter(x1.data.numpy()[:, 0], x1.data.numpy()[:, 1], 
                    c='b', label='class 1')
        w0, w1 = lr_net.features.weight[0]
        w0, w1 = float(w0.item()), float(w1.item())
        plot_b = float(lr_net.features.bias[0].item())
        plot_x = np.arange(-6, 6, 0.1)
        plot_y = (-w0 * plot_x - plot_b) / w1
        plt.xlim(-5, 7)
        plt.ylim(-7, 7)
        plt.plot(plot_x, plot_y)
        plt.text(-5, 5, 'Loss=%.4f' % loss.data.numpy(), 
                 fontdict={'size': 20, 'color': 'red'})
        plt.title("Iteration: {}\nw0:{:.2f} w1:{:.2f} b: {:.2f} accuracy:{:.2%}"
                  .format(iteration, w0, w1, plot_b, acc))
        plt.legend()
        plt.show()
        plt.pause(0.5)
        if acc > 0.99:
            break