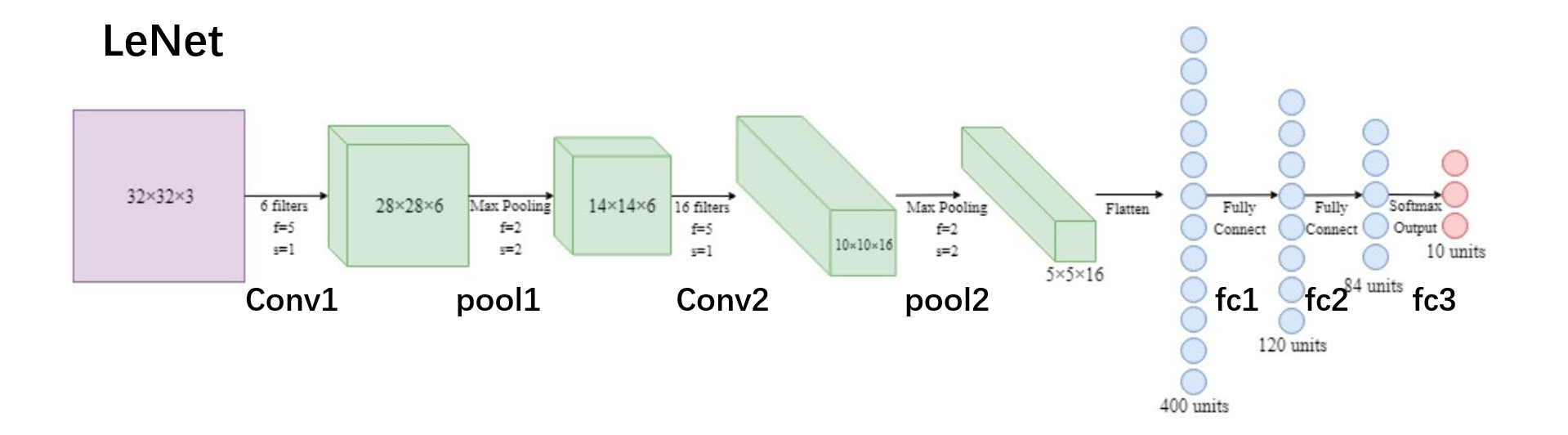
pytorch日积月累-模型建立

pytorch日积月累7-模型建立

1.1模型创建

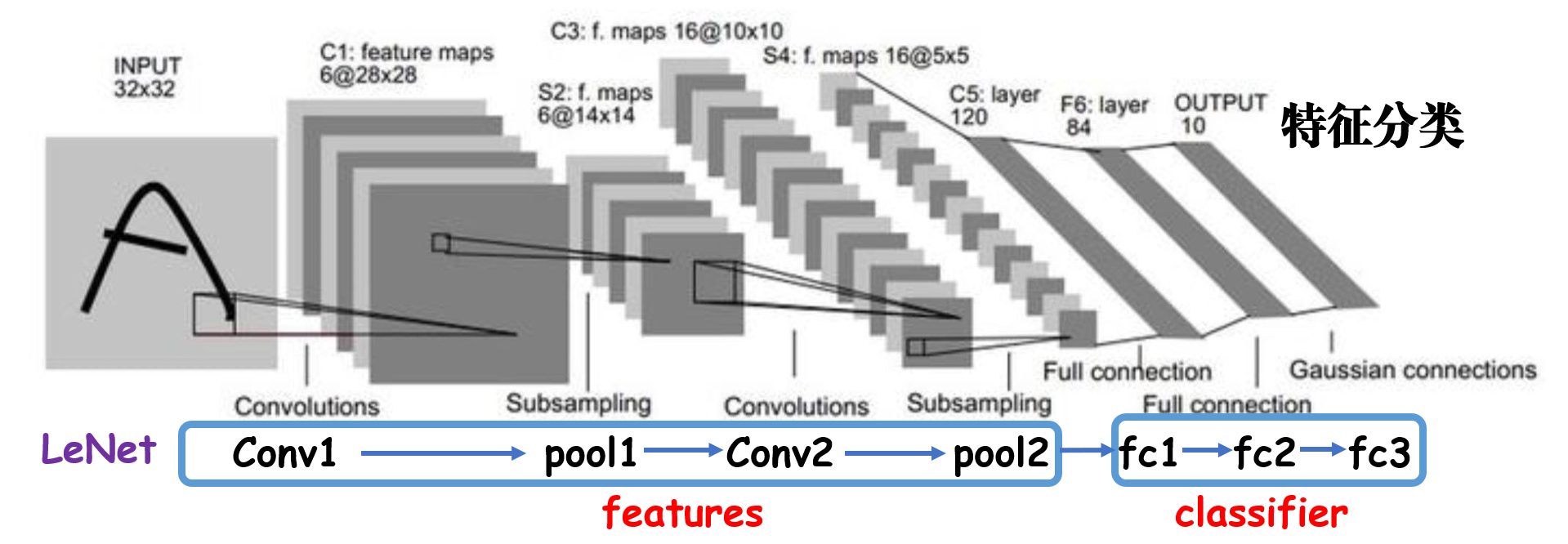
LeNet的计算图：（运算示意图）

模型创建步骤：

1.2torch.nn

torch.nn中包含以下四个主要部分：

• nn.Parameter：张量子类，表示可学习参数，如weight, bias

• nn.Module：所有网络层基类，管理网络属性

• nn.functional：函数具体实现，如卷积，池化，激活函数等

• nn.init：参数初始化方法

nn.Module中的八个字典：

• parameters : 存储管理nn.Parameter类

• modules : 存储管理nn.Module类

• buffers：存储管理缓冲属性，如BN层中的running_mean

• ***_hooks：存储管理钩子函数

self._parameters = OrderedDict()
self._buffers = OrderedDict()
self._backward_hooks = OrderedDict()
self._forward_hooks = OrderedDict()
self._forward_pre_hooks = OrderedDict()
self._state_dict_hooks = OrderedDict()
self._load_state_dict_pre_hooks = OrderedDict()
self._modules = OrderedDict()

nn.Module总结

• 一个module可以包含多个子module
• 一个module相当于一个运算，必须实现forward()函数
• 每个module都有8个字典管理它的属性

1.3模型容器Containers

模型容器Containers包含以下三个部分：

• nn.Sequetial 按顺序包装多个网络层
• nn.ModuleDict 像python的dict一样包装多个网络层
• nn.ModuleList 像python的list一样包装多个网络层

1.3.1 Sequential容器

Sequetial容器

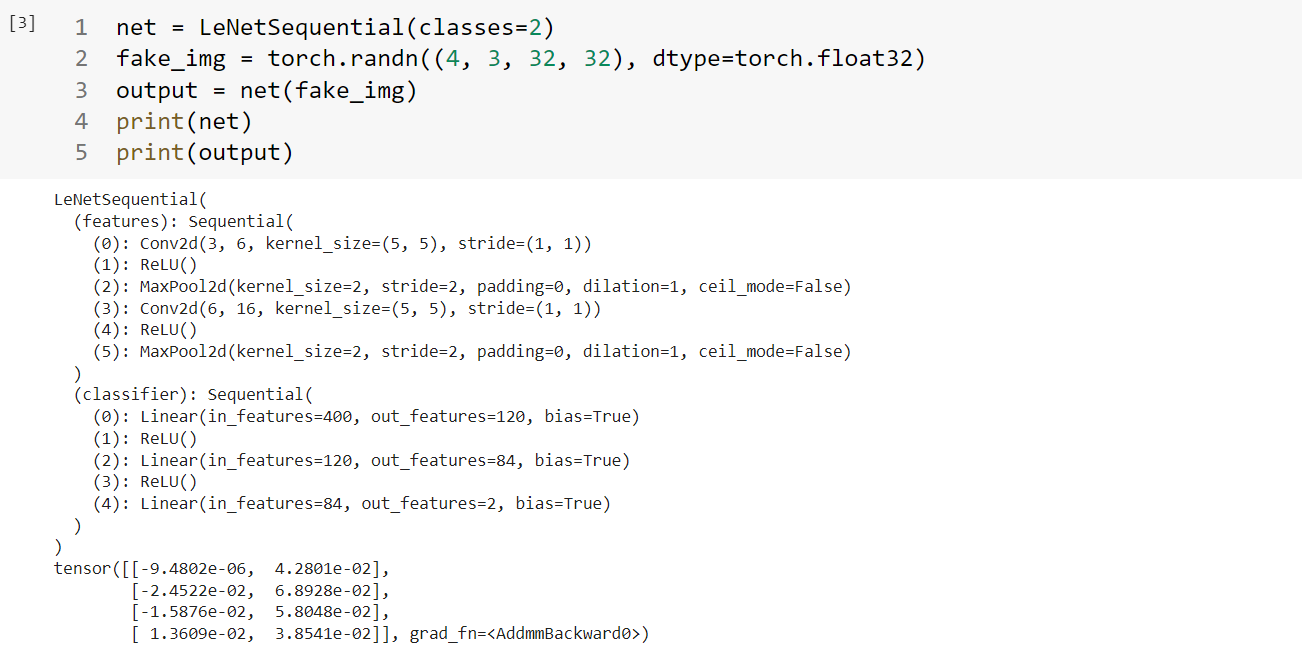
class LeNetSequential(nn.Module):
    def __init__(self, classes):
        super(LeNetSequential, self).__init__()
        
        self.features = nn.Sequential(
            nn.Conv2d(3, 6, 5),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2),
            nn.Conv2d(6, 16, 5),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2),
        )
        
        self.classifier = nn.Sequential(
            nn.Linear(16*5*5, 120),
            nn.ReLU(),
            nn.Linear(120, 84),
            nn.ReLU(),
            nn.Linear(84, classes),
        )
        
    def forward(self, x):
        x = self.features(x) #直接使用self.features(x)就可以实现六层的反向传播
        x = x.view(x.size()[0], -1)
        x = self.classifier(x)
        return x

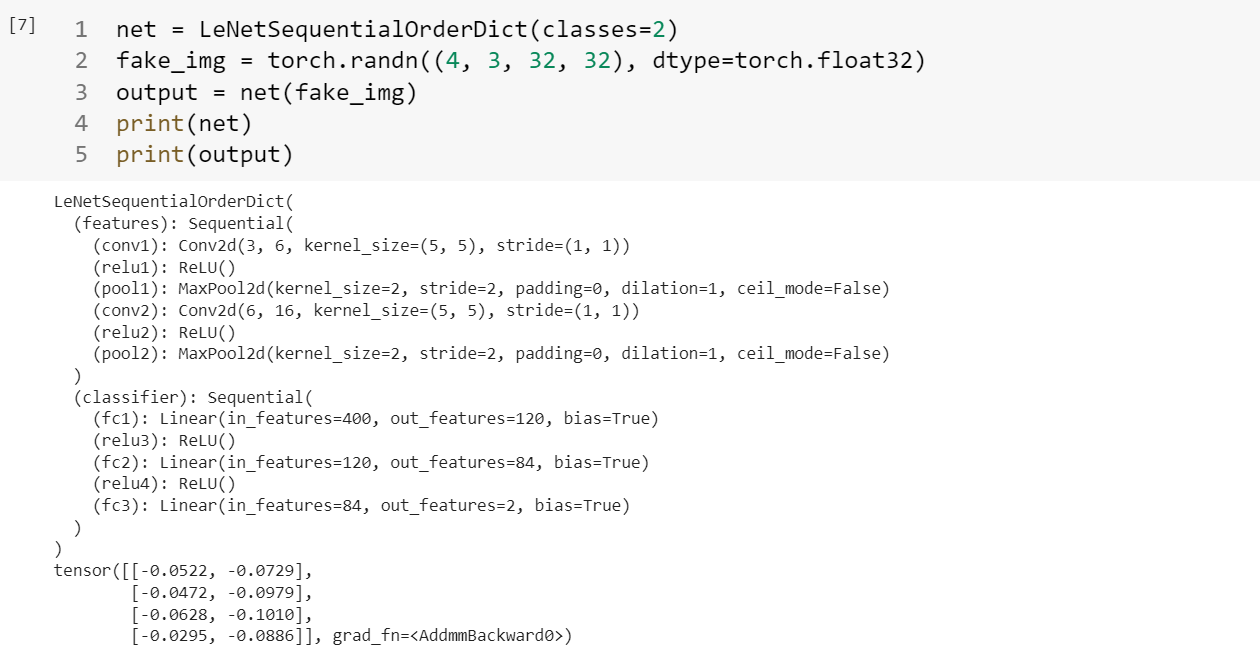
注意这种情况下每一层的输出都是按照序号来索引的，但是如果神经网络的层数很多的时候，这样的数字索引并不方便，所以采用下面的这种字典名称索引的方法：

from collections import OrderedDict
class LeNetSequentialOrderDict(nn.Module):
    def __init__(self, classes):
        super(LeNetSequentialOrderDict, self).__init__()
        self.features = nn.Sequential(OrderedDict({
            'conv1': nn.Conv2d(3, 6, 5),
            'relu1': nn.ReLU(),
            'pool1': nn.MaxPool2d(kernel_size=2, stride=2),
            'conv2': nn.Conv2d(6, 16, 5),
            'relu2': nn.ReLU(),
            'pool2': nn.MaxPool2d(kernel_size=2, stride=2),
        }))
        self.classifier = nn.Sequential(OrderedDict({
            'fc1':   nn.Linear(16*5*5, 120),
            'relu3': nn.ReLU(),
            'fc2':   nn.Linear(120, 84),
            'relu4': nn.ReLU(),
            'fc3':   nn.Linear(84, classes),
        }))
    def forward(self, x):
        x = self.features(x)
        x = x.view(x.size()[0], -1)
        x = self.classifier(x)
        return x

nn.Sequential 是nn.module的容器，用于按顺序包装一组网络层

• 顺序性：各网络层之间严格按照顺序构建

• 自带forward()：自带的forward里，通过for循环依次执行前向传播运算

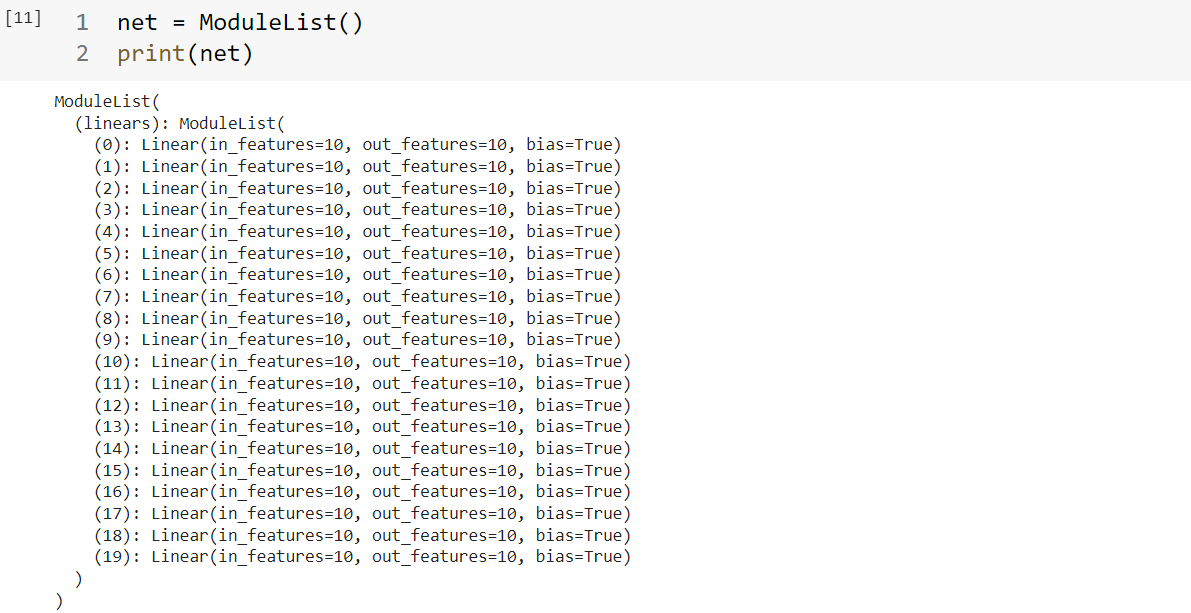
1.3.2 ModuleList容器

nn.ModuleList是nn.module的容器，用于包装一组网络层，以迭代方式调用网络层

主要方法：

• append()：在ModuleList后面添加网络层

• extend()：拼接两个ModuleList

• insert()：指定在ModuleList中位置插入网络层

class ModuleList(nn.Module):
    def __init__(self):
        super(ModuleList, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(10, 10) for i in range(20)])
    def forward(self, x):
        for i, linear in enumerate(self.linears):
            x = linear(x)
        return x

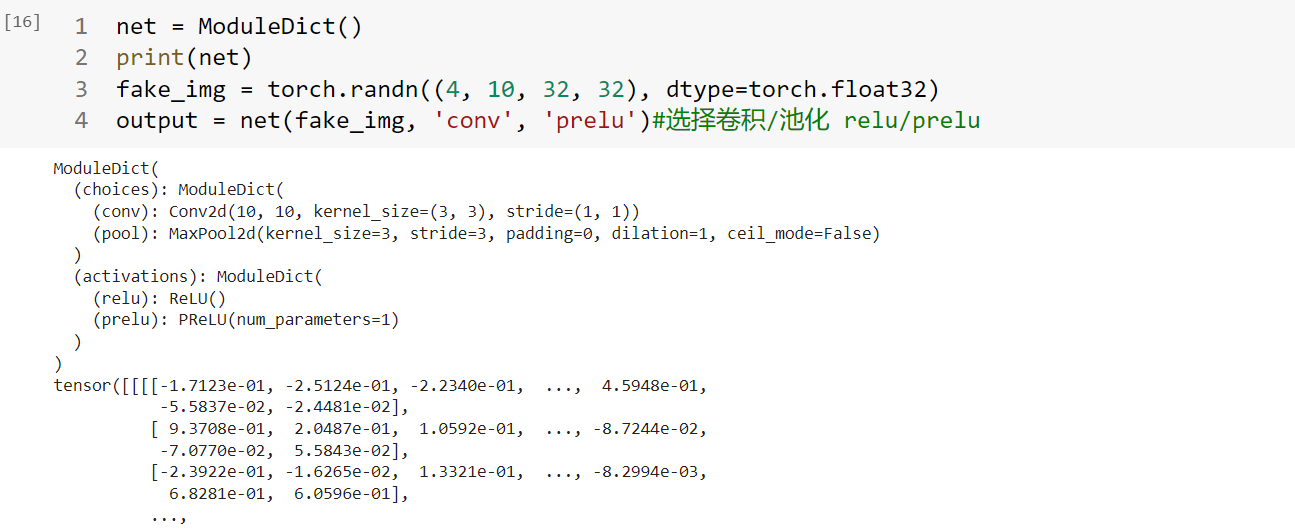
1.3.3 ModuleDict容器

是nn.module的容器，用于包装一组网络层，以索引方式调用网络层

主要方法：

• clear()：清空ModuleDict

• items()：返回可迭代的键值对(key-value pairs)

• keys()：返回字典的键(key)

• values()：返回字典的值(value)

• pop()：返回一对键值，并从字典中删除

class ModuleDict(nn.Module):
    def __init__(self):
        super(ModuleDict, self).__init__()
        self.choices = nn.ModuleDict({
            'conv': nn.Conv2d(10, 10, 3),
            'pool': nn.MaxPool2d(3)
        })
        self.activations = nn.ModuleDict({
            'relu': nn.ReLU(),
            'prelu': nn.PReLU()
        })
    def forward(self, x, choice, act):
        x = self.choices[choice](x)
        x = self.activations[act](x)
        return x

总结：

• nn.Sequential：顺序性，各网络层之间严格按顺序执行，常用于block构建
• nn.ModuleList：迭代性，常用于大量重复网构建，通过for循环实现重复构建
• nn.ModuleDict：索引性，常用于可选择的网络层

1.4AlexNet构建

import torchvision
alexnet = torchvision.models.AlexNet()#AlexNet源码如下

class AlexNet(nn.Module):
    def __init__(self, num_classes=1000):
        super(AlexNet, self).__init__()
        self.features = nn.Sequential(
            nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
            nn.Conv2d(64, 192, kernel_size=5, padding=2),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
            nn.Conv2d(192, 384, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(384, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(256, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
        )
        self.avgpool = nn.AdaptiveAvgPool2d((6, 6))
        self.classifier = nn.Sequential(
            nn.Dropout(),
            nn.Linear(256 * 6 * 6, 4096),
            nn.ReLU(inplace=True),
            nn.Dropout(),
            nn.Linear(4096, 4096),
            nn.ReLU(inplace=True),
            nn.Linear(4096, num_classes),
        )
    def forward(self, x):
        x = self.features(x)
        x = self.avgpool(x)
        x = torch.flatten(x, 1)
        x = self.classifier(x)
        return x

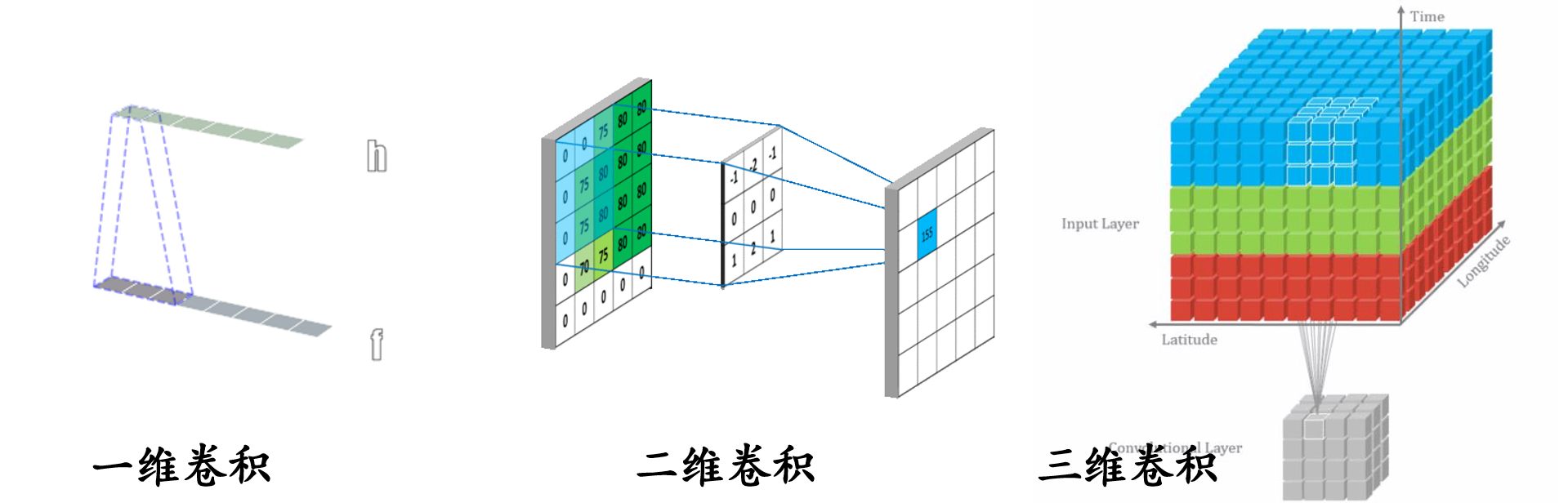
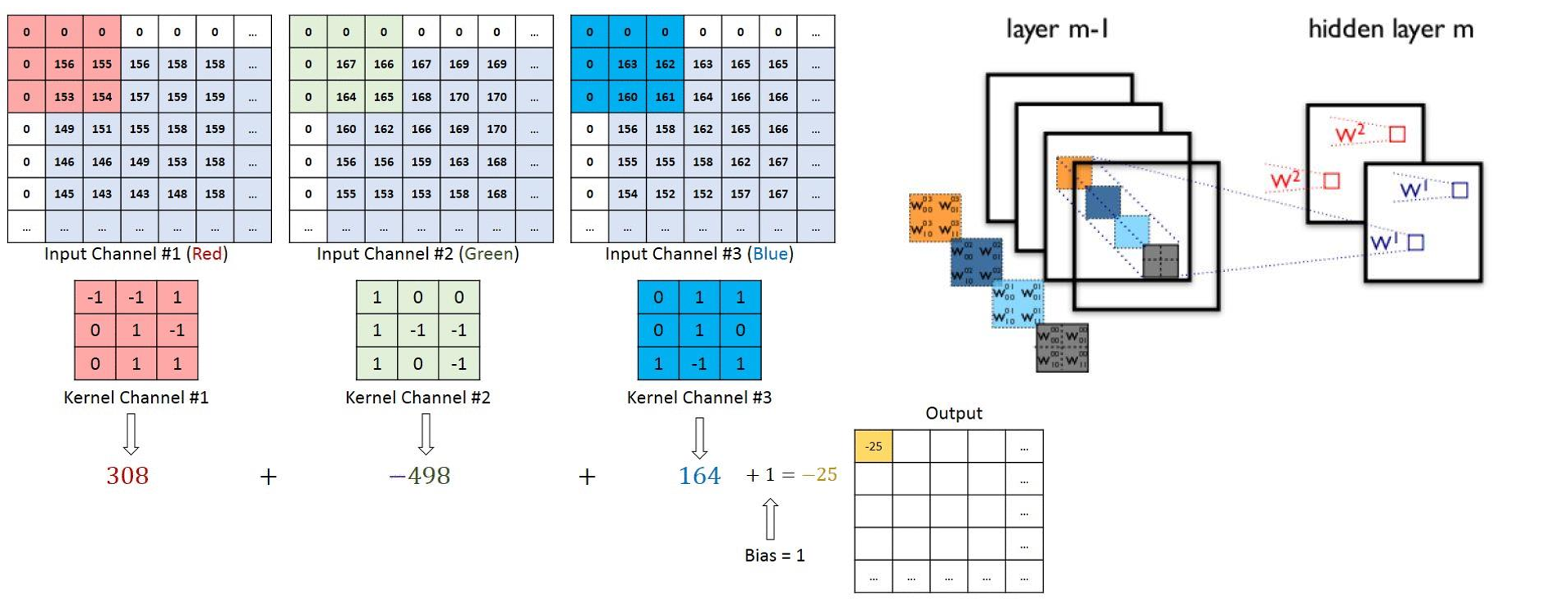
1.5卷积层

1.5.1 1d/2d/3d Convolution

卷积运算：卷积核在输入信号（图像）上滑动，相应位置上进行乘加

卷积核：又称为滤波器，过滤器，可认为是某种模式，某种特征。

卷积过程类似于用一个模版去图像上寻找与它相似的区域，与卷积核模式越相似，激活值越高，从而实现特征提取。

卷积维度：一般情况下，卷积核在几个维度上滑动，就是几维卷积。

1.5.2 nn.Conv2d

• 功能：对多个二维信号进行二维卷积
• 主要参数：

nn.Conv2d(in_channels,      #输入通道数
          out_channels,     #输出通道数，等价于卷积核个数
          kernel_size,      #卷积核尺寸
          stride=1,         #步长
          padding=0,        #填充个数,保证输入输出图像尺寸不变
          dilation=1,       #空洞卷积大小,卷积中有空格
          groups=1,         #分组卷积设置,常用于轻量化网络
          bias=True,        #偏置
          padding_mode='zeros')

尺寸计算：

• 简化版（！！！）

$$\text{out}_{s i z e}=\frac{\text{In}_{\text {size}}-\text {kernelsize}}{\text {stride}}+1$$

• 完整版：

$$H_{\text {out}}=\left\lfloor\frac{H_{\text {in}}+2 \times \text { padding }[0]-\text { dilation }[0] \times\left(\right.\text { kernel } \left._{\text {size }}[0]-1\right)-1}{\text { stride }[0]}+1\right ]$$

conv_layer = nn.Conv2d(3, 1, 3)   # input:(i, o, size) weights:(o, i , h, w)
nn.init.xavier_normal_(conv_layer.weight.data)
# calculation
img_conv = conv_layer(img_tensor)

卷积维度：一般情况下，卷积核在几个维度上滑动，就是几维卷积

转置卷积：

转置卷积又称为反卷积(Deconvolution)和部分跨越卷积(Fractionally strided Convolution) ，用于对图像进行上采样(UpSample)

为什么称为转置卷积？

假设图像尺寸为$4\times4$，卷积核为$3\times3$，padding=0，stride=1

• 正常卷积操作过程：图像：$I_{16\times1}$（先拉成向量）卷积核： $K_{𝟒\times𝟏𝟔}$ 输出：$O_{𝟒\times𝟏} = K_{𝟒\times𝟏𝟔} \times I_{𝟏𝟔\times1}$
• 转置卷积：假设图像尺寸为$2\times2$，卷积核为$3\times3$，padding=0，stride=1。图像：$I_{4\times1}$，卷积核：$K_{16\times4}$ ，输出：$O_{16\times𝟏} = K_{16\times4} \times I_{4\times1}$

nn.ConvTranspose2d( in_channels,
                    out_channels,
                    kernel_size,
                    stride=1,
                    padding=0,
                    output_padding=0,
                    groups=1,
                    bias=True,
                    dilation=1,
                    padding_mode='zeros')

尺寸计算简化版：

$$\mathrm{o u t}_{s i z e}=\left(\mathrm{in}_{s i z e}-1\right) \times\text {stride}+\mathrm{kernel}_{s i z e}$$

尺寸计算完整版：

$$H_{\text {out}}=\left(H_{\text {in}}-1\right) \times \operatorname{stride}[0]-2 \times \text { padding }[0]+\operatorname{dilation}[0] \times\left(\text { kernel }_{-} \operatorname{size}[0]-1\right)\\+\text { output_padding }[0]+1$$

conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2)   # input:(i, o, size)
nn.init.xavier_normal_(conv_layer.weight.data)
# calculation
img_conv = conv_layer(img_tensor)

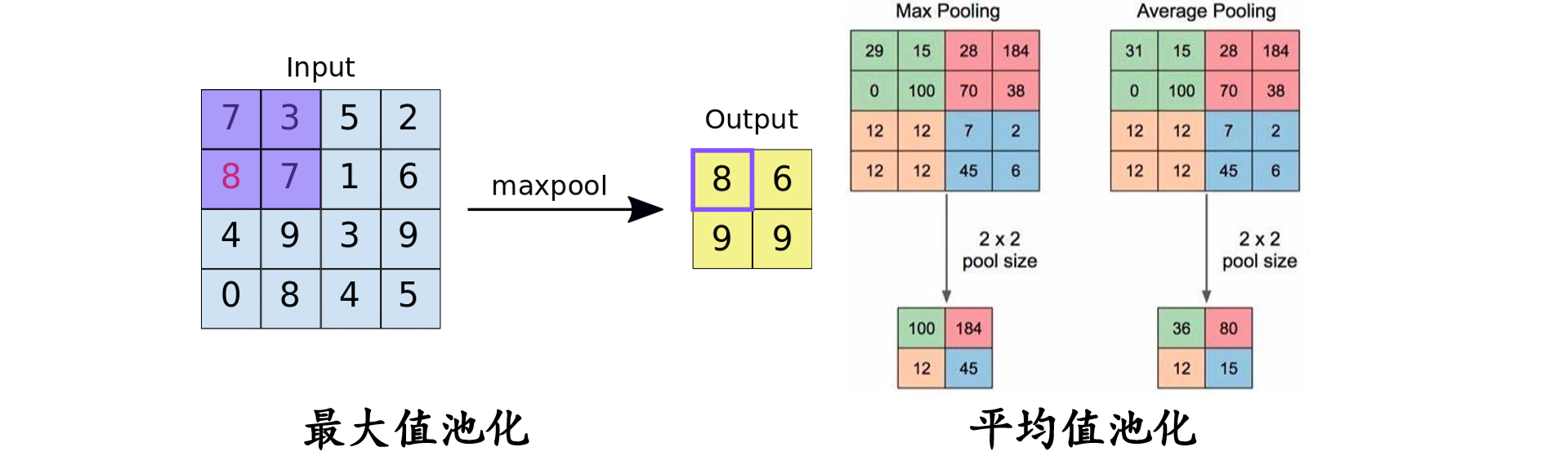
1.6池化层

池化运算：对信号进行收集”并“总结”，类似水池收集水资源，因而得名池化层

• “收集”：多变少
• “总结”：最大值/平均值

• nn.MaxPool2d()功能：对二维图像信息进行最大值池化。

#最大值池化
nn.MaxPool2d(kernel_size,            #卷积核尺寸 
             stride=None,            #步长
             padding=0,              #填充个数 
             dilation=1,             #池化核大小
             return_indices=False,   #记录池化像素索引 
             ceil_mode=False)        #尺寸向上取整

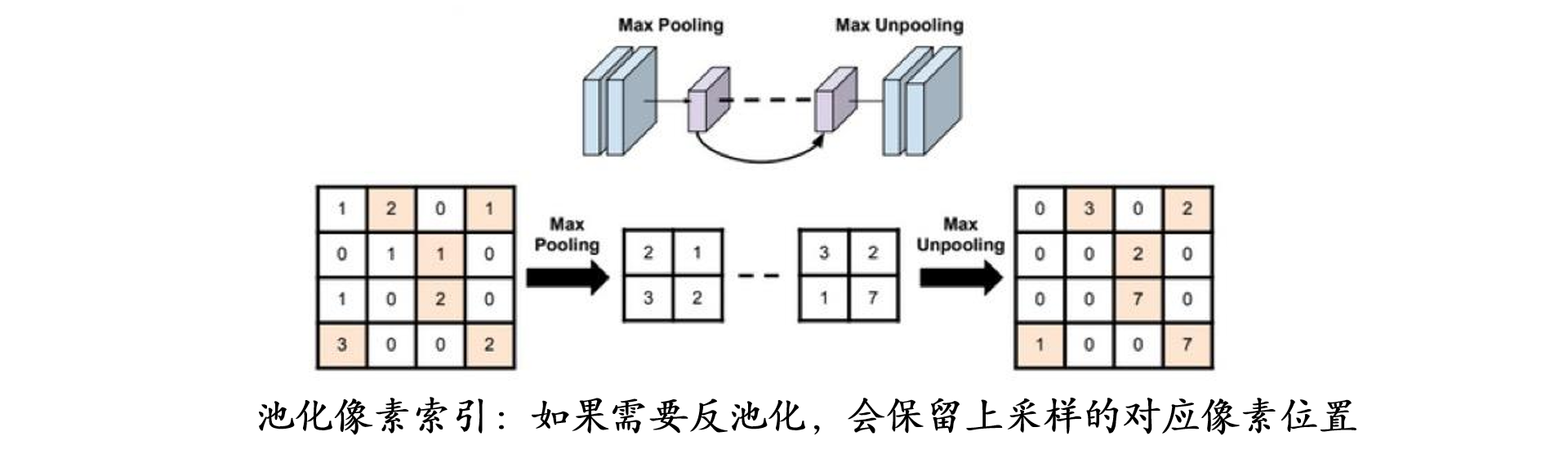
return_indices：记录池化像素索引，在反池化时，把对应的像素放在对应的位置上

maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2))   
# input:(i, o, size) weights:(o, i , h, w)
img_pool = maxpool_layer(img_tensor)

平均值池化：

nn.AvgPool2d(kernel_size, 
            stride=None, 
            padding=0, 
            ceil_mode=False,        #尺寸向上取整
            count_include_pad=True, #填充值用于计算
            divisor_override=None)  #除法因子

反池化：

• 功能：对二维信号（图像）进行最大值池化上采样

nn.MaxUnpool2d( kernel_size, #池化核尺寸
                stride=None, #步长
                padding=0)   #填充个数
forward(self, input, indices, output_size=None)

# pooling
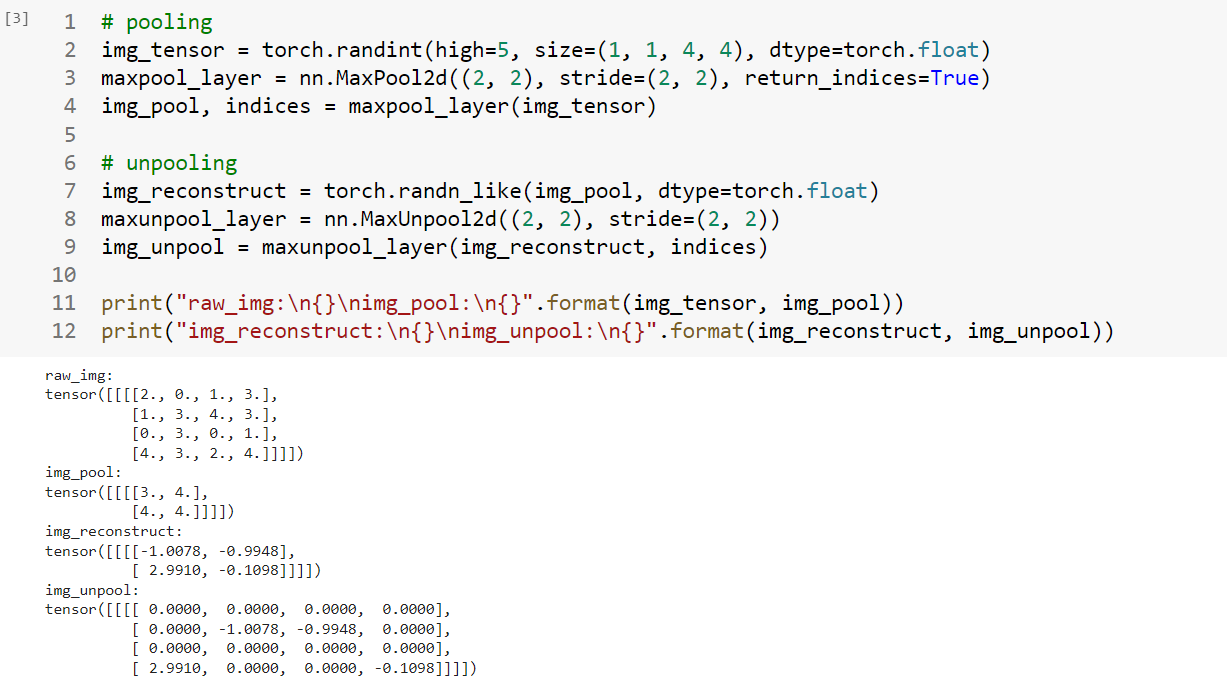
img_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float)
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True)
img_pool, indices = maxpool_layer(img_tensor)# 记录索引

# unpooling
img_reconstruct = torch.randn_like(img_pool, dtype=torch.float)
maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2))
img_unpool = maxunpool_layer(img_reconstruct, indices)

print("raw_img:\n{}\nimg_pool:\n{}".format(img_tensor, img_pool))
print("img_reconstruct:\n{}\nimg_unpool:\n{}".format(img_reconstruct, img_unpool))

可以观察到img_unpool矩阵中对应的时矩阵中进行最大值池化的位置。

1.7线性层

线性层又称全连接层，其每个神经元与上一层所有神经元相连实现对前一层的线性组合，线性变换。

• 功能：对一维信号（向量）进行线性组合

nn.Linear(in_features,  #输入结点数 
          out_features, #输出结点数
          bias=True)    #偏置

inputs = torch.tensor([[1., 2, 3]]) 
linear_layer = nn.Linear(3, 4)    #输入3，输出4
linear_layer.weight.data = torch.tensor([[1., 1., 1.],
                                         [2., 2., 2.],
                                         [3., 3., 3.],
                                         [4., 4., 4.]])
linear_layer.bias.data.fill_(0.5)
output = linear_layer(inputs)
print(inputs, inputs.shape)
print(linear_layer.weight.data, linear_layer.weight.data.shape)
print(output, output.shape)

通过结果可以发现，线性层本质是$y=x W^{T}+\text{bias}$，如第一列为$1\times1+1\times2+1\times3=6$

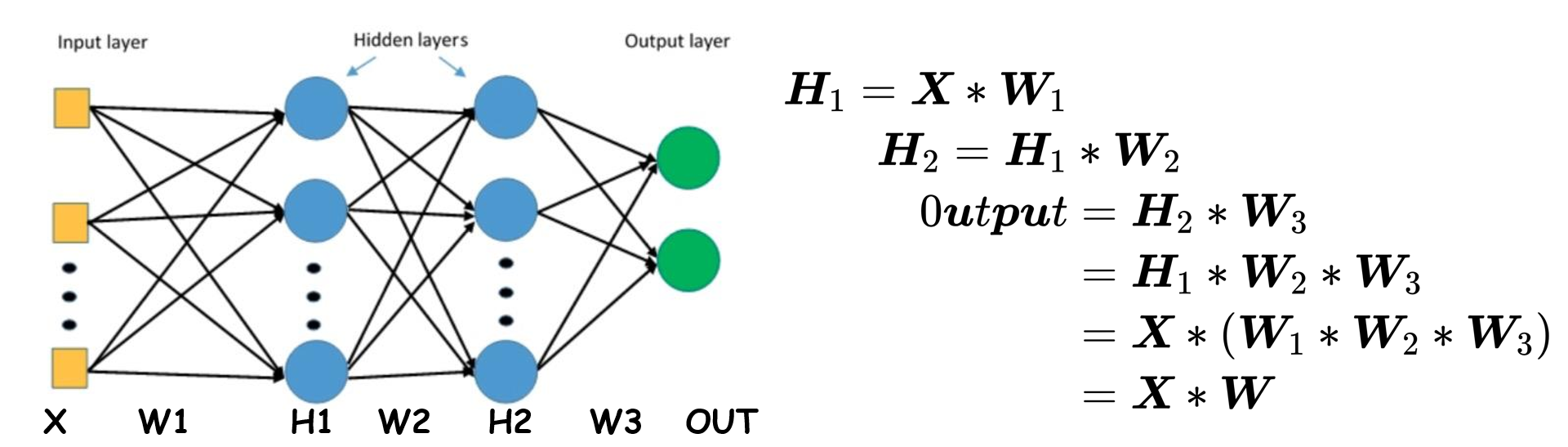
1.8激活函数层

激活函数对特征进行非线性变换，赋予多层神经网络具有深度的意义

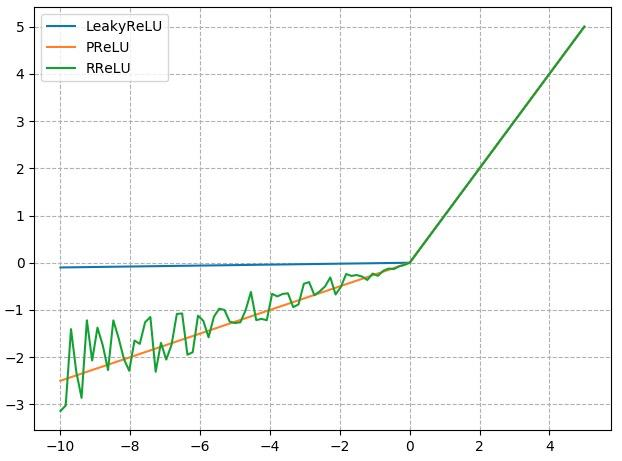
常用的激活函数：

nn.Sigmoid()
nn.tanh()
nn.ReLu()
nn.LeakyReLU()     #negative_slope: 负半轴斜率
nn.PReLU()         #init: 可学习斜率
nn.RReLU()         #lower: 均匀分布下限,upper:均匀分布上限