pytorch日积月累-权值初始化

pytorch日积月累8-权值初始化

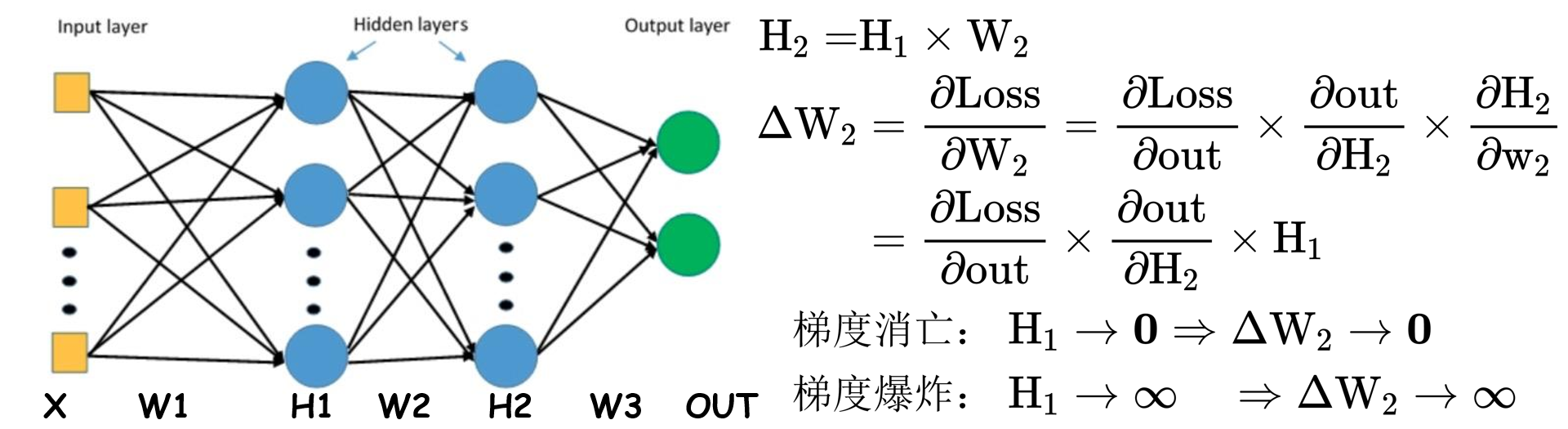
1.梯度消亡和梯度爆炸

$$1. \mathrm{E}(\boldsymbol{X} \times \boldsymbol{Y})=\boldsymbol{E}(\boldsymbol{X}) \times \boldsymbol{E}(\boldsymbol{Y})\\ 2. \mathrm{D}(\boldsymbol{X})=\boldsymbol{E}\left(\mathrm{X}^{2}\right)-[\boldsymbol{E}(\boldsymbol{X})]^{2} \\ 3. \mathbf{D}(\boldsymbol{X}+\boldsymbol{Y})=\boldsymbol{D}(\boldsymbol{X})+\boldsymbol{D}(\boldsymbol{Y}) \\$$

• ${D}({X} \times {Y})={D}({X}) \times {D}({Y})+{D}({X}) \times[E({Y})]^{2}+{D}({Y}) \times[{E}({X})]^{2}$
• 若$E({X})=0, {E}({Y})=0$，则有$\mathrm{D}(\mathrm{X} \times \mathrm{Y})=\mathrm{D}(\mathrm{X}) \times \mathrm{D}(\mathrm{Y})$

已知$H_1$层输出的结果$\mathrm{H}_{11}=\sum_{i=0}^{n} X_{i} \times W_{1 i}$,根据$\quad \mathrm{D}(\mathrm{X} \times \mathrm{Y})=\mathrm{D}(\mathrm{X}) \times \mathrm{D}(\mathrm{Y})$,可以得到：

$$\begin{array}{c} \mathbf{D}\left(\mathrm{H}_{11}\right)=\sum_{i=0}^{n} D\left(X_{i}\right) \times D\left(W_{1 i}\right) \\ =\mathrm{n} \times(1 \times 1) \\ =\mathrm{n} \\ \operatorname{std}\left(\mathrm{H}_{11}\right)=\sqrt{\mathbf{D}\left(\mathrm{H}_{11}\right)}=\sqrt{n} \\ \mathbf{D}\left(\mathrm{H}_{1}\right)=n \times D(X) \times D(W)=1 \\ \mathbf{D}(W)=\frac{1}{n} \Rightarrow \operatorname{std}(W)=\sqrt{\frac{1}{n}} \end{array}$$

可以发现对于神经网络，每一层的标准差都变为原来的$\sqrt{n}$倍。

def initialize(self):
   for m in self.modules():
       if isinstance(m, nn.Linear):#采用恰当的权值初始化方法
          nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))    
        # normal: mean=0, std=1

2.Xavier初始化

带有激活函数时如何进行初始化：

方差一致性：保持数据尺度维持在恰当范围，通常方差为1

激活函数：饱和函数，如Sigmoid，Tanh

$$n_{i} \times D(W)=1 \\ n_{i+1} \times D(W)=1 \\ \Rightarrow D(W)=\frac{2}{n_{i}+n_{i+1}}$$ $$W \sim U[-a, a] \\ D(W)=\frac{(-a-a)^{2}}{12}=\frac{(2 a)^{2}}{12}=\frac{a^{2}}{3} \\ \frac{2}{n_{i}+n_{i+1}}=\frac{a^{2}}{3} \Rightarrow a=\frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}} \\ \Rightarrow \quad W \sim U\left[-\frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}, \frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}\right]$$

#利用公式进行的初始化方法
a = np.sqrt(6 / (self.neural_num + self.neural_num))
tanh_gain = nn.init.calculate_gain('tanh')
a *= tanh_gain
nn.init.uniform_(m.weight.data, -a, a)

#nn模块中的Xavier初始化方法
tanh_gain = nn.init.calculate_gain('tanh')
nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)

3.Kaiming初始化

方差一致性：保持数据尺度维持在恰当范围，通常方差为1

激活函数：ReLU及其变种

$$\mathbf{D}(W)=\frac{2}{n_{i}} \\ \mathbf{D}(W)=\frac{2}{\left(1+\mathrm{a}^{2}\right) \times n_{i}} \\ \operatorname{std}(W)=\sqrt{\frac{2}{\left(1+\mathrm{a}^{2}\right) \times n_{i}}}$$

nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num))

nn.init.kaiming_normal_(m.weight.data)

计算方差变化尺度：

nn.init.calculate_gain(nonlinearity, param=None)
#nonlinearity: 激活函数名称
#param: 激活函数的参数，如Leaky ReLU的negative_slop

x = torch.randn(10000)
out = torch.tanh(x)
gain = x.std() / out.std()
print('gain:{}'.format(gain))
tanh_gain = nn.init.calculate_gain('tanh')
print('tanh_gain in PyTorch:', tanh_gain)#1.666667表示方差每次会减少1.6左右