论文笔记--使用菲涅耳衍射模型进行人类呼吸检测

使用菲涅耳衍射模型进行人类呼吸检测

论文原文：《From Fresnel Diffraction Model to Fine-grained Human Respiration Sensing with Commodity Wi-Fi Devices》

这篇是2022年寒假在实验室实习的时候阅读的论文，当时还很稚嫩，浅浅记录一下

1.摘要

【背景】在什么位置，细微的呼吸可以被检测到，为什么其他位置不能被检测到。目前还没有提供任何理论来指导系统的设计，研究人员不得不依靠试错的方法来使系统工作。

• 首次利用菲涅尔衍射模型精确地量化了衍射增益和人类目标体的细微胸部位移之间的关系，从而成功地将先前认为的第一菲涅尔区(FFZ)的“破坏性”阻塞衍射转化为有益的感知能力。
• 不仅考虑了现有的解决方案中胸部正面位移，而且也考虑了背面的微小位移，成为第一个清楚地解释背后的理论性能的区别躺和坐着呼吸感应的模型，我们能够清楚地解释为什么躺着通常比坐着具有更好的呼吸感知能力。
• 通过两个廉价的商品Wi-Fi卡，每个卡都只配备一个天线，我们能够在FFZ中60%以上的位置实现高于98%的呼吸速率监测精度。
• 我们能够在每个位置的第一菲涅尔区内提出传感能力的细节热图，以指导呼吸感应用户清楚地知道呼吸监测的好位置，如果位于一个糟糕的位置，如何移动稍微达到一个好位置。

1.Introduction

• 这是第一次应用菲涅耳衍射模型进行FFZ内的人体呼吸监测和分析。本研究为室内环境中细粒度人和物体运动感知提供了一般的理论基础。
• 通过分析FFZ内移动的一个物体如何影响接收到的射频信号，并将一个人类目标建模为一个不同大小的圆柱体，我们开发了一个数学模型，将自己的位置与FFZ内呼吸的可检测性联系起来。
• 我们发现了FFZ内部呼吸感知的多种独特特性：
  • 虽然胸部前侧运动占主导地位，但背部运动确实影响感知能力
  • 由于身体厚度的差异，$A$人良好的呼吸感知位置可能不是$B$人的好位置；
  • 视线(LoS)位置有利于躺卧情景呼吸感知，但不利于坐着。

2. 理解菲涅耳衍射模型

当目标位于FFZ内时，衍射比反射强得多，因此衍射主导。

2.1 菲涅耳衍射模型的基础知识

【菲涅尔区简介】

​ 假设$P_1$和$P_2$是一对无线射频收发设备，菲涅尔区是指对应于以收发设备为焦点的一簇同心椭圆。对于给定波长$\lambda$的无线信号，其包含$n$层同心椭圆的菲涅尔区依据公式：$|P_1Q_n|+|Q_nP_2|-|P_1P_2|=n\lambda/2$，其中$Q_n$是第$n$层椭圆的轨迹，菲涅尔区可以有无数层，最内层的椭圆被定义为第一菲涅尔区，其特点是发射路径$P_1Q_1P_2$的长度比直线传播路径$P_1P_2$长半个波长$\lambda/2$。

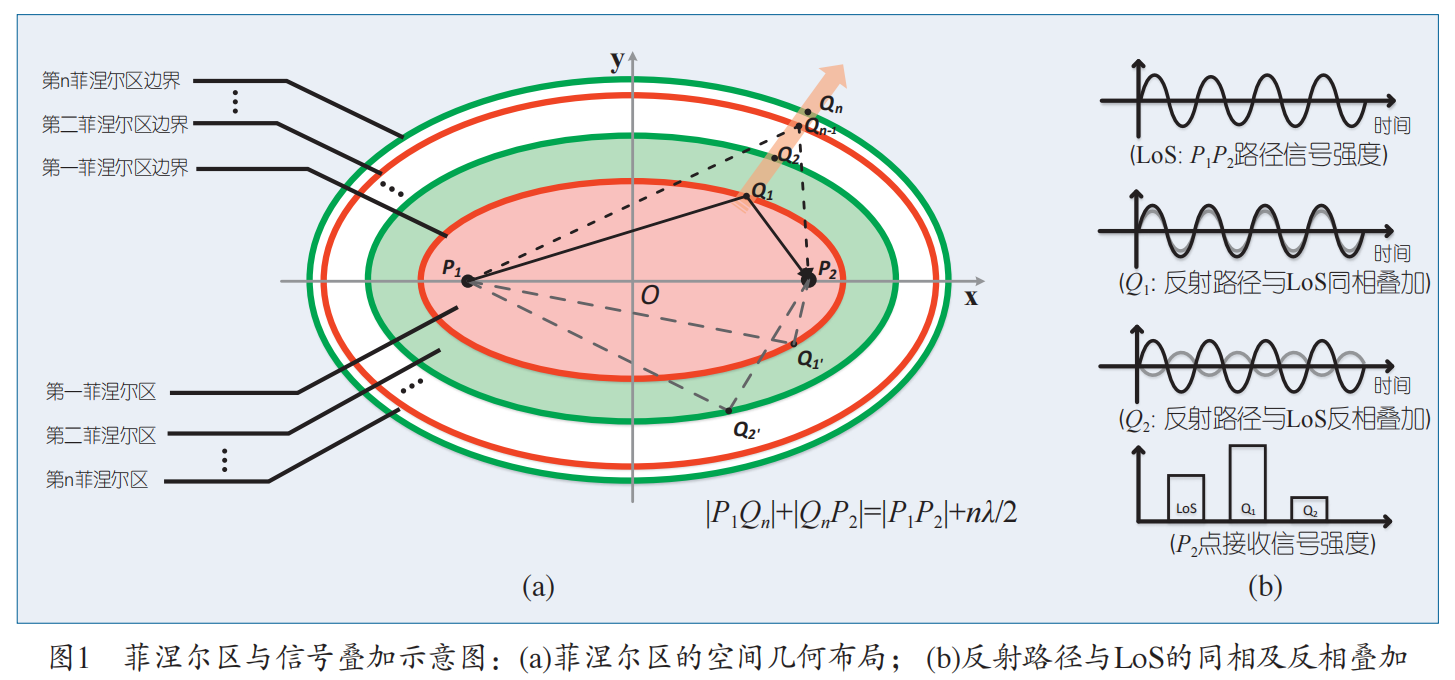
​ 我们关注第一菲涅耳区，因为超过70%的能量通过这个区转移。假设在自由空间场景中，当目标在这个区域移动时，接收信号的振幅和相位会受到很大的影响。发送设备$T$和接收设备$R$之间的射频（Radio Frequency，RF，PS：针对中频和基带区分）信号波长为$\lambda$，两设备连线中有一点为$O$，$|TO|=d_1,|RO|=d_2$，在用$h$表示$Q$到$O$的垂直距离，$|QO|=h$，信号经过$Q$点时产生衍射。

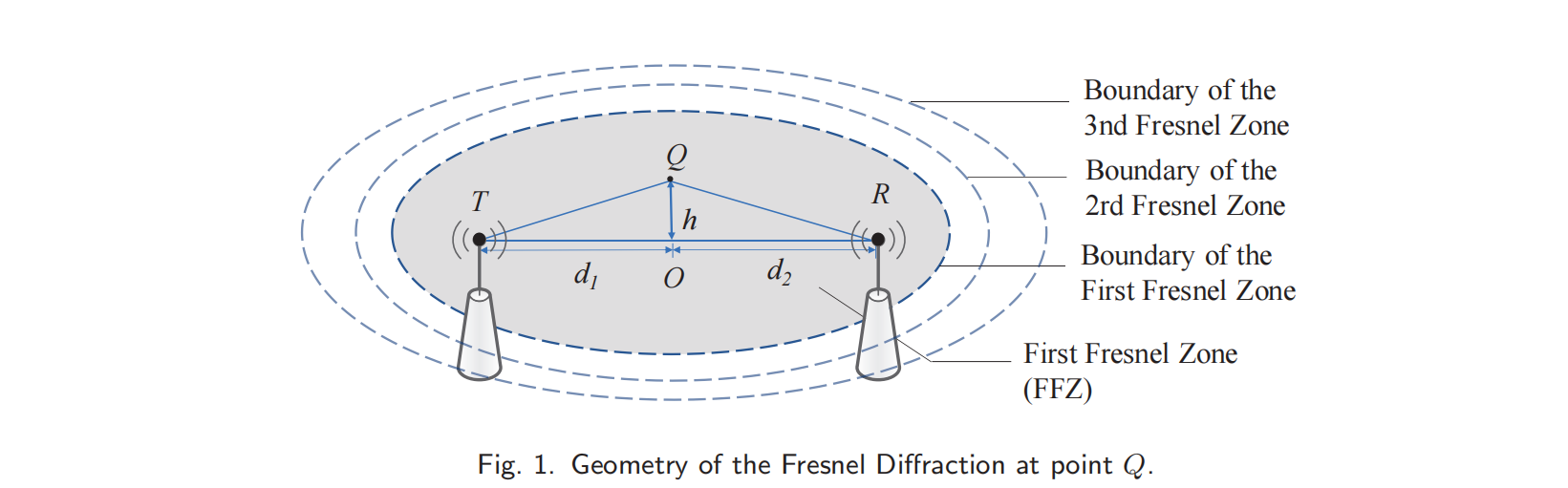
TQR和TOR的路径差：

$$\begin{array}{l} \Delta d=|T Q R|-|T O R| \\ =\sqrt{\left(d_{1}\right)^{2}+\left(h^{2}\right)}+\sqrt{\left(d_{2}\right)^{2}+\left(h^{2}\right)}-\left(d_{1}+d_{2}\right) \\ =d_{1} \sqrt{1+\left(h / d_{1}\right)^{2}}+d_{2} \sqrt{1+\left(h / d_{2}\right)^{2}}-\left(d_{1}+d_{2}\right) \end{array}$$

在FFZ中$\left(h / d_{1}\right)^{2} \ll 1$和$ \quad\left(h / d_{2}\right)^{2} \ll 1 $，根据近似$\left(\sqrt{1+x} \approx 1+\frac{x}{2}, x \ll1)\right. $，可以得到：

$$\Delta d \approx \frac{h^{2}}{2} \frac{\left(d_{1}+d_{2}\right)}{d_{1} d_{2}} \\$$

在信号传播的情况下，由该路径差$\Delta d$引起的相应相位差为：

$$\varphi=\frac{2 \pi \Delta d}{\lambda}=\pi h^{2} \frac{\left(d_{1}+d_{2}\right)}{\lambda d_{1} d_{2}}$$

菲涅耳-基尔霍夫衍射参数(The Fresnel-Kirchhoff diffraction parameter)$v$定义为：

$$v=h \sqrt{\frac{2\left(d_{1}+d_{2}\right)}{\lambda d_{1} d_{2}}}$$

因此，相位差可以简化为：$\varphi=\frac{\pi}{2} v^{2}$与从T到R的直接路径信号相比，这种额外的相位变化发生在通过Q的衍射信号处。

2.2 一个移动的目标如何影响射频信号？

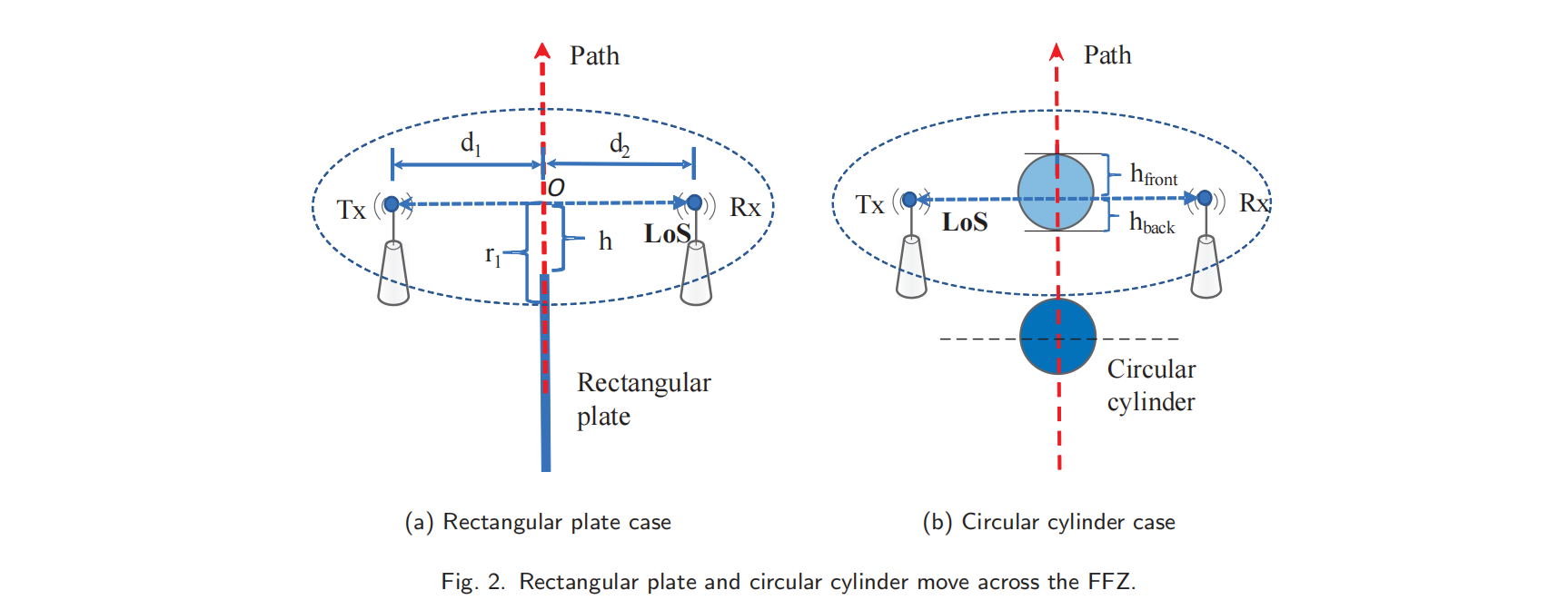
实际上，该目标具有不可忽视的规模。我们首先分析当金属板穿过FFZ时，信号是如何变化的。为了研究板的一侧边缘的衍射效应，我们假设金属板有无限的长度，只有一侧移动。FFZ的短轴$r_1$可以表示为（FFZ的边界公式为$|T_xQ_1|+|Q_1R_x|-|R_xT_x|=\frac{\lambda}{2}$）：

$$r_{1}=\sqrt{\frac{\lambda d_{1} d_{2}}{d_{1}+d_{2}}}$$

我们进一步定义了一个参数$u$，称为菲涅耳间隙，来表示交叉的百分比：$u=\frac{h}{r_1}$​，其中$h$是从$O$到金属板边缘的矢量距离。

• 当板边缘刚好接触到两个收发器的LoS时，$h=0$。
• 当板的边缘第一次FFZ的边界时，$h=−r_1$。
• 当板到达边界的另一边时，$h=r_1$。

所以$u$在-1到1的范围内。根据这一定义，菲涅耳-基尔霍夫衍射参数$v$可以用菲涅耳间隙$u$表示为：

$$v=h \sqrt{\frac{2\left(d_{1}+d_{2}\right)}{\lambda d_{1} d_{2}}}=h \frac{\sqrt{2}}{r_{1}}=\sqrt{2} u$$

因此，接收端由于衍射引起的信号振幅可以表示为：

$$F(v)=\frac{1+j}{2} \cdot \int_{v}^{\infty} \exp \left(\frac{-j \pi z^{2}}{2}\right) d z$$

其中$F(v)$被称为菲涅耳积分。由于金属板的存在而引起的衍射增益是由$\text{Gain}_{\text{Diff}}=20\log |F(v)|$ 给出。实际上，人类目标的规模是有限的。当一个人出现在FFZ中时，这些信号在人体的两侧都有衍射。因此，我们接下来研究了一个有限尺寸的圆柱体的衍射效应（一个直径为12厘米)，当它穿过FFZ时。圆筒沿着两个收发器的垂直平分线移动，如图（b）所示。

我们定义两个新的参数：菲涅耳前间隙$u_{front}$和菲涅耳后间隙$u_{back}$。圆柱体的衍射效应由两部分组成（由正面和背面引起的衍射）。

• 菲涅耳前间隙$u_{front}$反映了目标的正面在FFZ内的相对位置。$h_{front}$表示从圆柱体前侧到收发器LoS的矢量距离。因此菲涅耳前积分为：

$$F\left(v_{\text {front }}\right)=\frac{1+j}{2} \cdot \int_{v_{\text {front }}}^{\infty} \exp \left(\frac{-j \pi z^{2}}{2}\right) d z$$

同理，菲涅尔后积分表示为：

$$F\left(v_{\text {back }}\right)=\frac{1+j}{2} \cdot \int_{-\infty}^{v_{\text {back }}} \exp \left(\frac{-j \pi z^{2}}{2}\right) d z$$

所以，有限尺寸的圆柱存在的整体衍射增益由下面表示：

$$G a i n_{\text {Diff }}=20 \log \left|F\left(v_{\text {front }}\right)+F\left(v_{\text {back }}\right)\right|$$

2.3 通过基准实验进行验证

实验设置：

• 两个Wi-Fi收发器间隔100厘米。采用长度为150cm的滑动轨道将金属板平滑地进入FFZ。
• 该金属板的尺寸为$100\times100$厘米。实验中使用的两个圆柱状圆柱体的直径分别为6cm和12cm，而圆柱体的长度均为20cm。
• 在实验中，每个收发器配备有三个天线，但只有一个天线用于传输/接收。这两个收发器上的天线被放置在同一高度。在实验中，我们将两个天线的高度调整为离地面65厘米和110厘米。滑动轨迹与收发器的垂直平分线对齐。中心载波频率为5.24GHz，信号波长为5.7 cm

基准实验：为了验证FFZ中的衍射效应，我们沿着滑动轨道移动了金属板，随着菲涅耳间隙参数$u$从-2变化到2。在轨道上，金属板将首先接触到第三菲涅耳区的边界，然后再接触到第二菲涅耳区的边界。然后到达FFZ的边界，最后到达两个收发器的LoS。在那之后，它逐渐地离开了FFZ。根据$\text{Gain}_{\text{Diff}}=20\log |F(v)|$​ ，我们得到了理论上的衍射增益。在接触FFZ的边界之前，我们观察到在第三和第二菲涅耳区边界附近的一个峰和一个谷(即，在$u=−1.73$和$u=−1.41$)。靠近FFZ边界的峰值出现在FFZ内部的$u=−0.85$。然后振幅一直在下降，直到结束。 如图（a）所示：

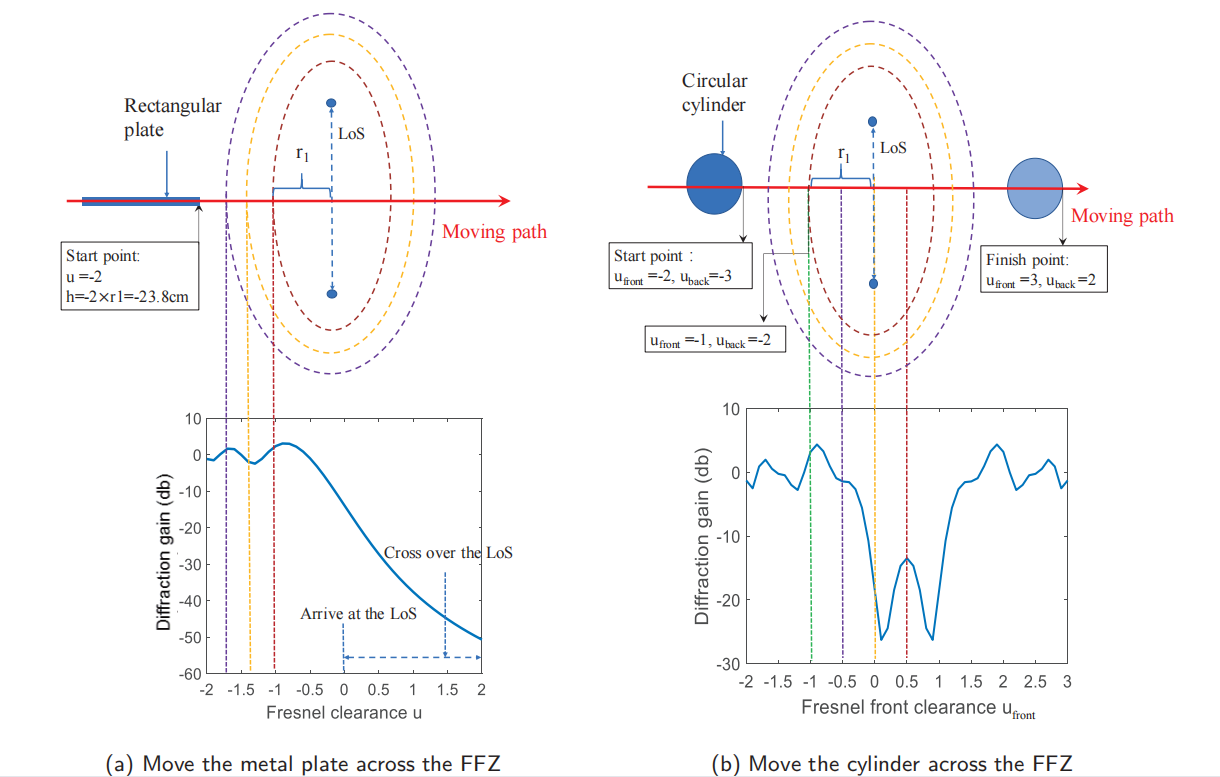
接下来，我们让直径为12厘米的圆柱体沿着两个收发器的垂直平分线移动，从菲涅耳前间隙$u_{front}=-2$开始，停止在菲涅耳前间隙$u_{front}=3$.通过用等式计算菲涅耳前后积分，衍射增益如图(b)所示。在圆柱体接触LoS之前，振幅也会经历一个峰值和一个谷值。当圆柱体的正面移动到FFZ的前半部分的中间点($u_{front}=-0.5$)时，振幅有一个较短的平台，然后迅速下降，直到圆柱体到达LoS。有趣的是，当圆柱体穿过覆盖LoS后，振幅再次增加，直到圆柱体达到$u_{front}=0.5$(圆柱体的重心在LoS上)。整体形状关于$u_{front}=0.5$呈对称模式。

2.4 从菲涅耳衍射模型中揭示的关键特性

• FFZ的边界不一定是最高能量的点。峰值出现在进入FFZ后的一个轻微位置。这促使我们了解到，最好的和最差的感知位置可能并不位于FFZ边界上。
• 小尺寸的物体在位于FFZ内部时具有双面衍射。对于圆柱体，穿过FFZ过程中的衍射增益是非单调的。当圆柱体的重心位于LoS上时，底部就会出现局部峰值。这一特性解释了为什么当目标坐着时，呼吸感知的良好位置会交替出现。
• 不同直径的物体的衍射效应略有不同，导致峰值的大小和位置不同。所以，不同体型的人可能在FFZ的同一位置具有不同的感知能力。

3.在FFZ中感知人类的呼吸

• 根据两种常见的场景为人体进行建模：

  • 躺在床上
  • 坐在椅子上

• 基于上一节的观察结果，为这两种情况提出了两种不同的模型。

• 将胸部位移转换为细粒度的信号相位变化，以表征人类的呼吸过程。
• 通过对每个小网格的感知能力的仔细研究，能够呈现出躺着和坐姿的呼吸感知能力热图。同时，展示了身体厚度和呼吸深度对呼吸感知的影响。

3.1 建立人体呼吸模型

呼吸过程中前胸移动在4.2-5.4mm，后部移动在2.5-2.6mm，中外侧尺寸为0.6-1.1mm。在深吸气屏气(DIBH)时，胸部位移可增加到前后尺寸为12.6毫米。

我们模拟人体躺在床上和分别坐在椅子上，因为它们在呼吸过程中非常不同。人体被建模为一个不同大小的平面圆柱体，如图（a）。其中外圆柱体和内圆柱体表面分别对应于吸入和呼气的胸部位置。

考虑到图中一个人体躺在收发器之间的床上，如图（c），呼吸过程类似于金属板进出移动，位移约为5毫米。

人体和金属板之间的关键区别在于，人体主体具有不可忽视的宽度。

the multiple knife-edge diffffraction theory：FFZ中许多障碍物的影响相当于如图b所示的单一最高障碍物。

通过这种方式，我们可以在躺下的场景中模拟一个在FFZ中有微小运动的平板。

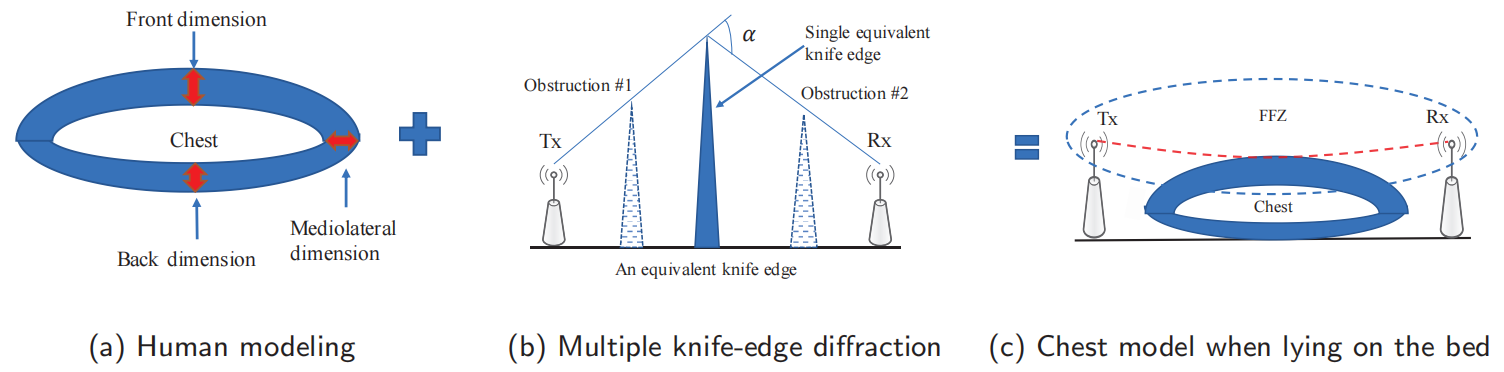
接下来，我们坐在椅子上模拟人体。胸部模型仍然是一个不同大小的圆柱体。然而，与躺在床上不同的是，现在都需要考虑前后尺寸的胸部位移。受我们将一个坐姿或站立的人体呼吸建模为一个圆柱体，前运动尺寸为5毫米，背部尺寸为3毫米。当受试者坐在FFZ中时，两侧发生衍射。菲涅耳正面和背面间隙在计算精细呼吸感应的衍射增益时都应该考虑。

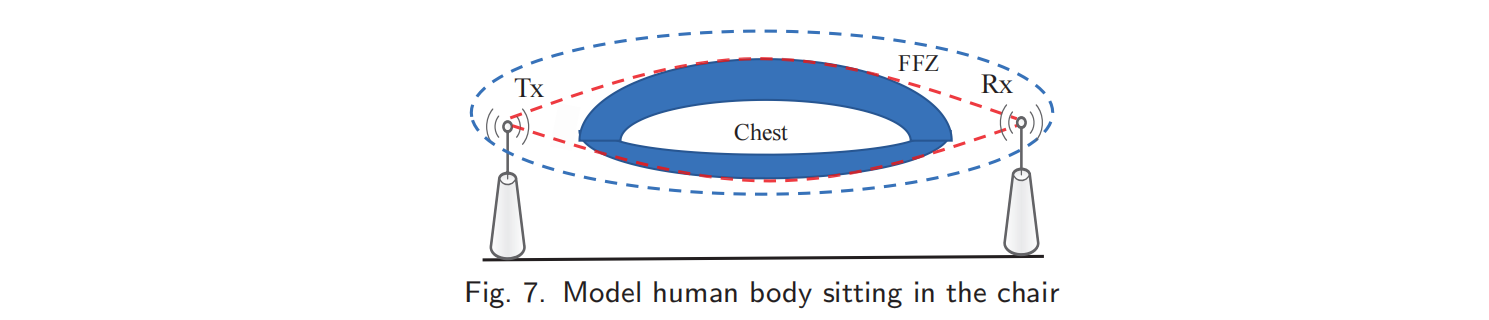
3.2 将胸部位移转换为相变

首先将胸部位移转换为衍射路径长度的变化，然后将这个路径长度的变化转换为相变。假设胸部位移为$\Delta d$，由运动引起的路径长度变化在$2\Delta d$左右。一个波长的路径变化显示出$2\pi$的相位变化。因此，由呼吸作用引起的相位旋转$\theta$被计算为：

$$\theta=2 \pi \times \frac{2 \Delta d}{\lambda}$$

其中$\lambda$是波长。对于普通呼吸和深呼吸，胸腔位移量$\Delta d$分别为5mm和12mm，对应的相变为$60^{\circ} $和$150^{\circ} $。

如图，由呼吸引起的振幅变化高度依赖于FFZ中的目标位置。相同数量的胸部位移会导致非常不同的振幅变化。

• 当胸部移位发生在单调间隔时，由呼吸引起的接收信号波动较大。
• 在非单调区间内，波动较弱，因此更容易被噪声淹没。

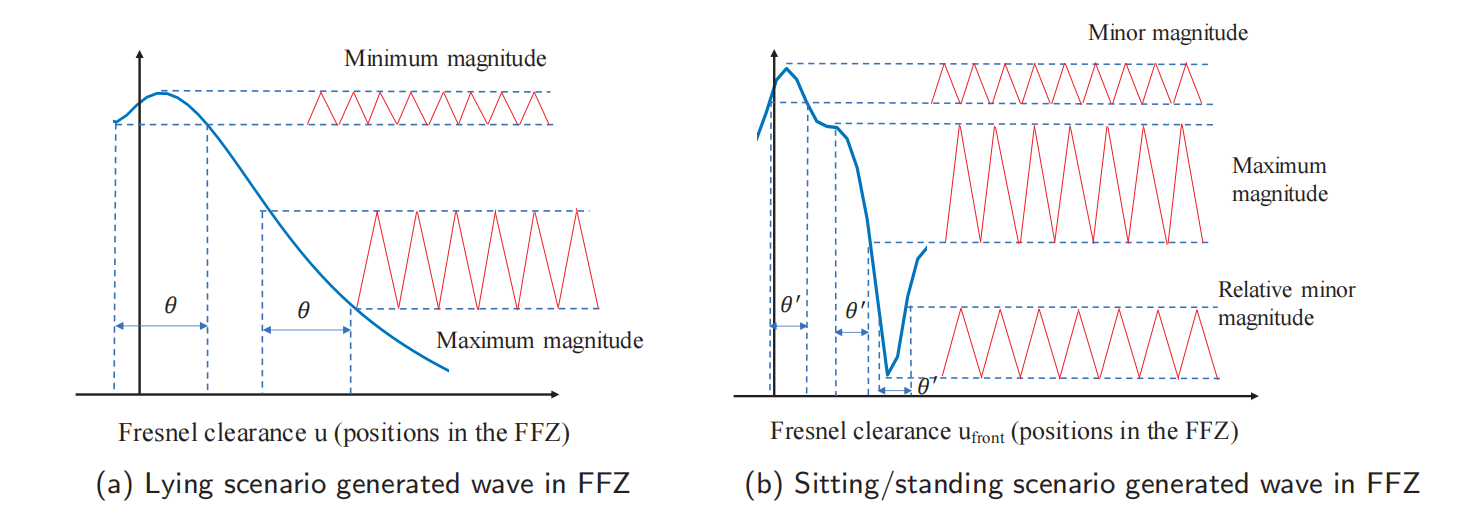
3.3 FFZ内胸部位置的影响

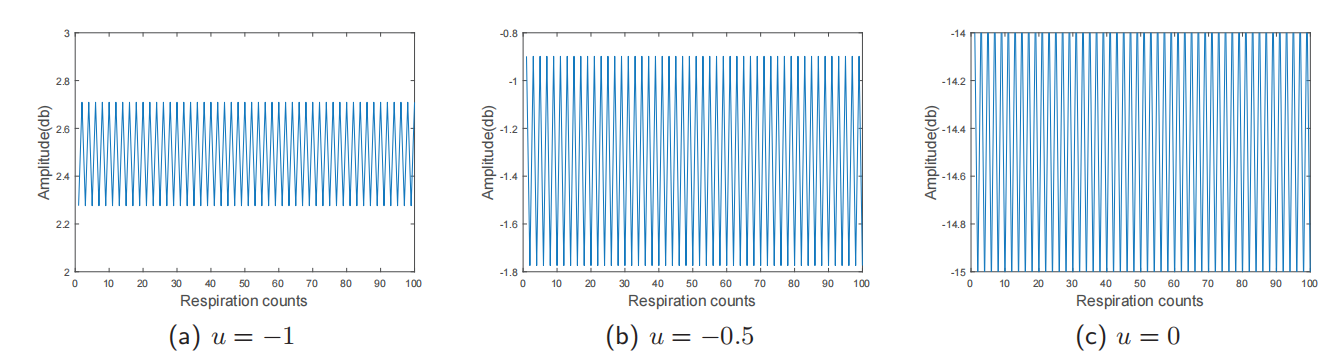
如上图，可以看出，FFZ$(u=−1)$的边界并不是一个适合呼吸感知的好位置。当胸腔前端移动到半椭圆的中间$(u=−0.5$)并进一步接触LoS时，其可检测性明显增强。

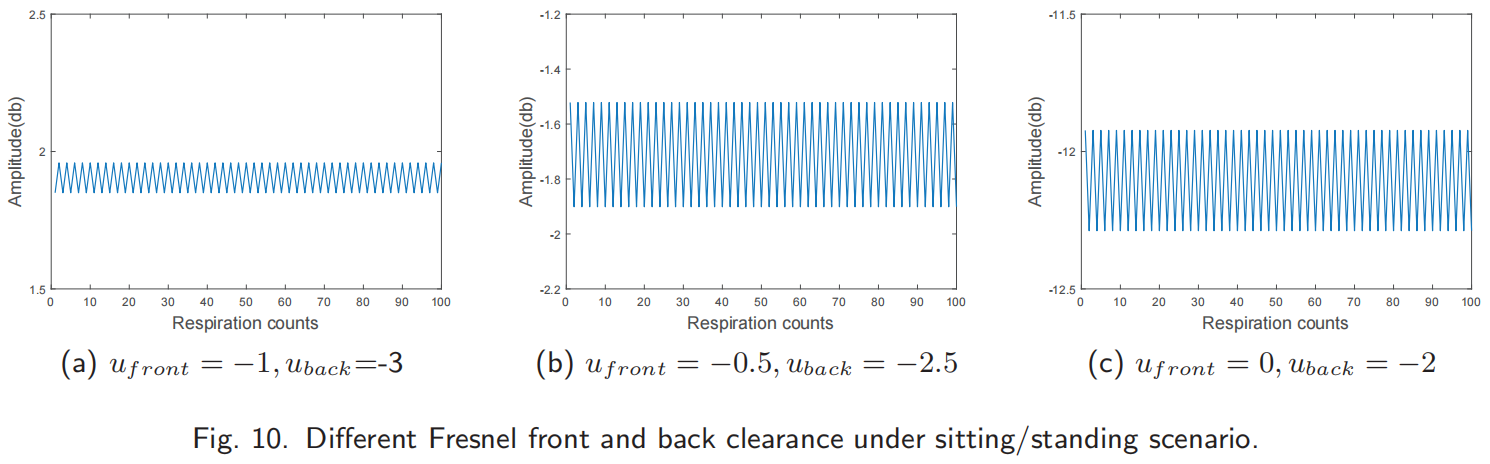
上图显示了坐/站场景中的信号变化。虽然FFZ的边界也是一个不好的位置，但在内部移动会呈现出更大的变化，因此具有更好的感知性能。

（3.4）身体厚度的影响： 对A来说好位置对B来说可能不是好位置。

（3.5 ）被试者与收发器的距离的影响：更靠近收发器并不是提高感知能力的有效方法。